

The solution will look something like this.
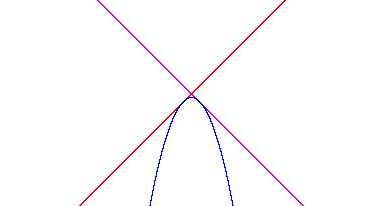
To make things simple, let's try to make a parabola that has a vertex on the y-axis. This means that the parabola will be symmetric about the y-axis. To make the graphs of our linear functions look like the lines in the picture above, the slopes of our lines need to have equal magnitudes but opposite signs. Therefore, we know that a = -c. Thus, we also know that the parabola opens down.
In the picture above, we also see that the two lines cross directly above the vertex of the parabola. Since we are choosing the vertex to be on the y-axis, we know that these two lines will cross each other on the y-axis. Therefore, their y-intercepts must be the same, or b = d.
Since we know a = -c and b = d, we can how write
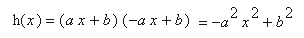
We can differentiate h to find the slope of the tangent lines.
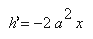
Now we know the slope of the tangent lines from taking the derivative of h, but we also know that the slope of the two tangent lines are a and -a, respectively. Thus, we now have
where x1 is the x value of the point where the parabola and one of the lines intersect. Dividing through by a yields
We can find x1 by setting the equation for the parabola and the equation for the line equal to each other and solving for x1.
Dividing through by ax1 + b yields
Substituting this into equation (1), we see
Now we have a family of functions that satisfy the conditions listed above.
Here is an example when a = 1.
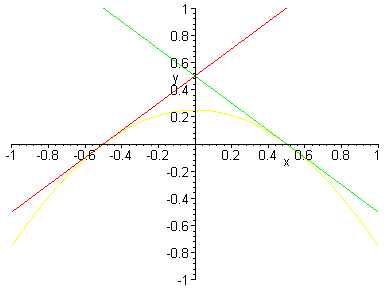
These two lines appear to be tangent to the parabola, but let's check.
f(x) = x + 1/2, and g(x) = - x + 1/2. Therefore, h(x) = - x2 + 1/4.
The graphs of the functions f and h intersect at the point (-1/2, 0). The derivative of h at x = -1/2 is 1, which is the same as the coefficient of x in f.
The graphs of the functions g and h intersect at the point (1/2, 0). The derivative of h at x = 1/2 is -1, which is the same as the coefficient of x in g.
Thus, our functions satisfy the conditions listed above.
Let a = 1/2. Then
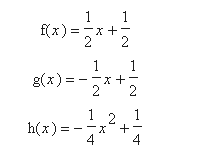
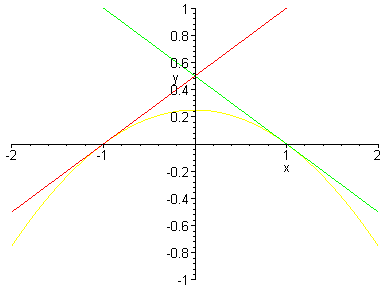
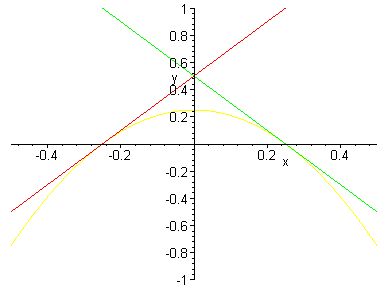
Let a = 2. Then
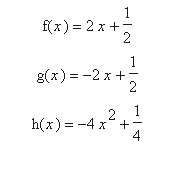
I will not answer these questions in this write-up, but they are good extensions to this problem.
1. Must the tangent lines have slopes of equal magnitude but opposite sign?
2. Must the tangent lines cross directly above the vertex of the parabola?
3. Must the parabola open down?
4. Must the parabola be symmetric about the y-axis?