

Assignment 7 deals with tangent circles. In this write-up, I will focus on the construction of the circles that are tangent to two given circles in each case. In each construction, I will also examine the locus of the center of the circle that is constructed, and I will examine the lines that are tangent to the locus. Finally, I will discuss the locus the of midpoint of a very important segment in each construction.
We will investigate the following problem:
Given two circles and a point on one of the circles, construct a circle that is tangent to the two circles with one point of tangency being the designated point.
Case One
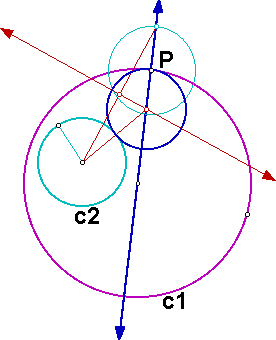
For the circles c1 and c2 below, we want to construct a circle tangent to both of the circles with one point of tangency being P. In the diagram below, we want to construct the blue circle.
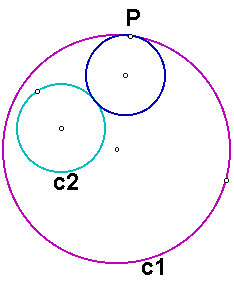
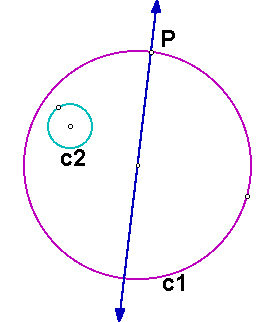
We know that the center of the desired circle will lie along a line from the center of c1 to the point P, as below.
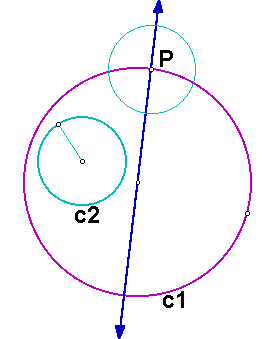
Now we can construct a circle with center P with the same radius as circle c2.
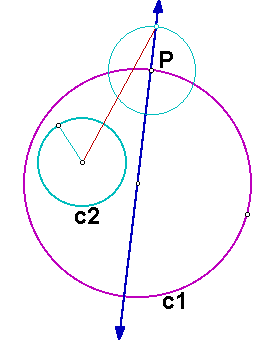
Using the intersection point (that is outside of circle c1) of the line and the new circle as one endpoint and the center of circle c2 as the other endpoint, we can construct the base of an isosceles triangle.
To find the other vertex of the isosceles triangle, we can construct the perpendicular bisector of the segment we just created. The intersection of the perpendicular bisector and the original line gives us the other vertex. This is the center of our desired circle.
Click here for a GSP sketch of the construction.
Click here for a GSP script for the construction.
Sound like magic? Click here to go to Assignment 7, where you will find the motivation behind this construction.
The Locus of the Center
Let us consider the locus of the centers of all such circles tangent to the two given circles. If we trace the center of the circle that is tangent to the given circles as we move the point P around the circle C1, we see the following locus of the center of the center of all such circles tangent to the two given circles.
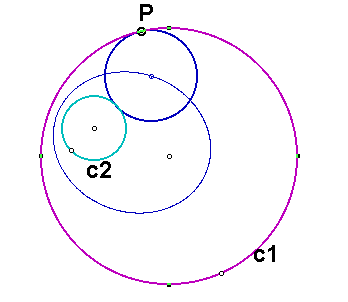
Click here for a GSP sketch that lets you watch the animation.
The locus appears to be an ellipse. Why is it an ellipse, though?
If we construct segments connecting the center of the constructed circle to the center of each of the given circles, we see that the sum of the lengths of these two segments is the same as the sum of the lengths of the radii of the two given circles. Since this sum is a constant, the locus of the center of all such circles tangent to two given circles is an ellipse with foci at the centers of the two given circles.
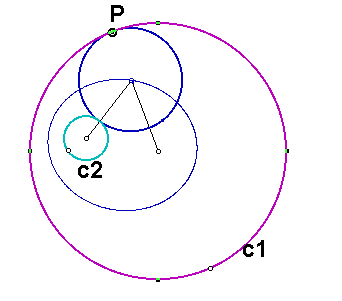
Click here for a GSP sketch that lets you watch the animation with the two segments.
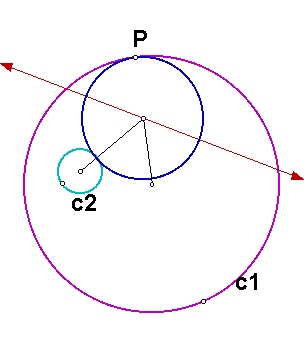
In the above diagram, the red line is always tangent to the locus. It forms an envelope of lines that are all tangent to the ellipse.
Click here to see the animation.
Case Two
For the circles c1 and c2 below, we want to construct a circle tangent to both of the circles with one point of tangency being P. We want the smaller circle to be inside the constructed circle. In the diagram below, we want to construct the blue circle.

As before, we know that the center of the desired circle will lie along a line from the center of c1 to the point P, and we can construct a circle with center P with the same radius as c2
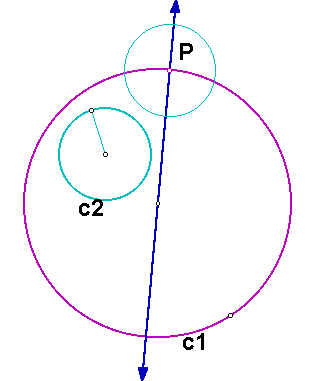
Using the intersection point of the line and the new circle as one endpoint and the center of circle c2 as the other endpoint, we can construct the base of an isosceles triangle. In this case, though, we want to use the intersection point that is inside circle c1. As before, to find the other vertex of the isosceles triangle, we can construct the perpendicular bisector of the segment we just created. The intersection of the perpendicular bisector and the original line gives us the other vertex. This is the center of our desired circle.
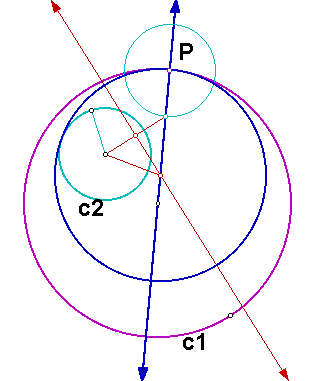
Click here for a GSP sketch of the construction.
Click here for a GSP script for the construction.
The Locus of the Center
Let us consider the locus of the center of all such circles tangent to the given circles. Let's trace the center of the constructed circle as P moves around circle C1.
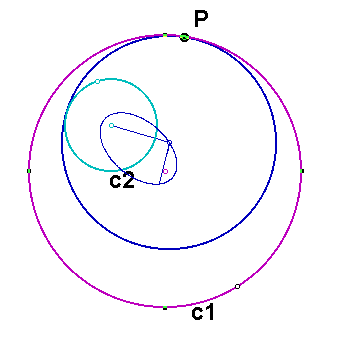
Click here for a GSP sketch that includes the animation.
If we construct the segments joining the center of the constructed circle to the centers of the given circles, we see that the sum of the lengths of these two segments is the same as the difference of the lengths of the radii of the two given circles. Since this difference is constant, the locus of the center is again an ellipse with foci at the centers of the two given circles.
Case 3
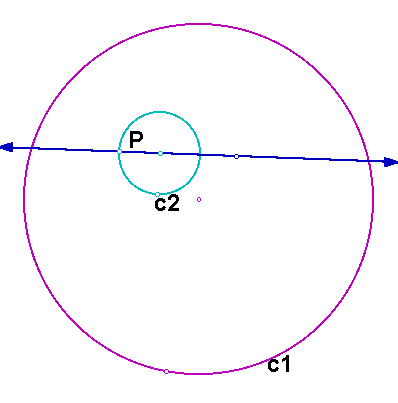
In the next case that we want to consider, the point P is on the smaller circle. We want to construct a circle tangent to the two given circles such that the smaller circle is outside the constructed circle. In the diagram below, we want to construct the blue circle.
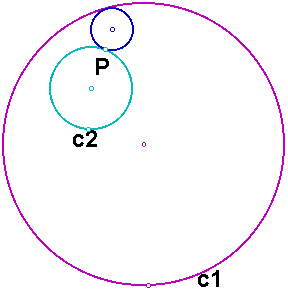
The construction is not very different from the construction in case 1, and the resulting circle is exactly the same. First, construct a line through the center of circle c2 and the point P.
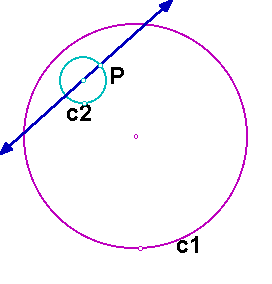
Next we construct a circle with center P and the same radius as circle C1. The segment having the center of c1 as one endpoint and the intersection point (that is farthest from c2) of the new circle and the first line as the other endpoint forms the base of an isosceles triangle.
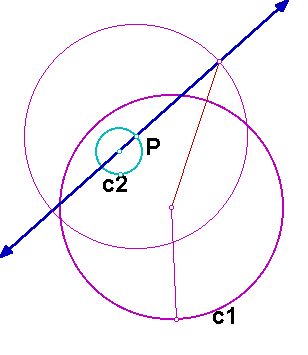
We can construct the isosceles triangle, and the other vertex of the triangle is the center of the desired circle.
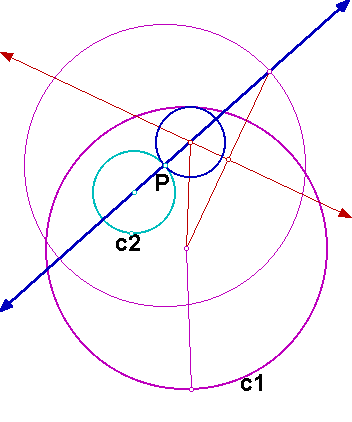
Click here for a GSP sketch.
Click here for a GSP script.
The Locus of the Center
The circles that are created in this case are the same as the circles in case one. Therefore, the locus of the center is the same ellipse.
Click here to see the animation.
Click here to see an animation that includes the envelope of lines for the ellipse.
Case 4
In the next case that we want to consider, the point P is again on the smaller circle. We want to construct a circle tangent to the two given circles such that the smaller circle is inside the constructed circle. In the diagram below, we want to construct the blue circle.

The construction is not very different from the construction in case 2, and the resulting circle is exactly the same. First, construct a line through the center of circle c2 and the point P.
Next we construct a circle with center P and the same radius as circle C1. The segment having the center of c1 as one endpoint and the intersection point (that is closest to c2) of the new circle and the first line as the other endpoint forms the base of an isosceles triangle. We can construct the isosceles triangle, and the other vertex of the triangle is the center of the desired circle.
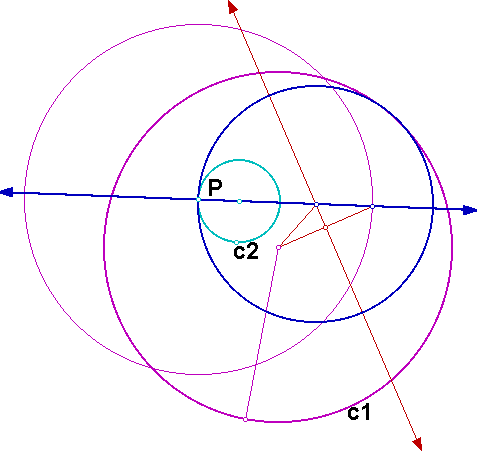
Click here for a GSP sketch.
Click here for a GSP script.
The Locus of the Center
The circles that are created in this case are the same as the circles in case two. Therefore, the locus of the center is the same ellipse.
Click here to see the animation.
Click here to see an animation that includes the envelope of lines for the ellipse.
Case 5
Next let us consider the case where the two circles intersect. First let's construct the circle that is tangent to both circles and either inside one of the circles. This construction is similar to cases 1 and 3. For example, in the diagram below, we want to construct the blue circle.
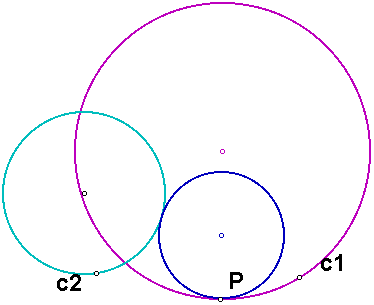
First, we construct the line through the center of c1 and the point P. Then we construct the circle having center P and the same radius as circle c2.
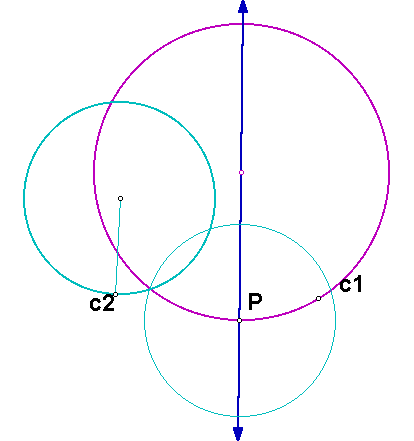
Using the intersection point (that is farthest from c2) of this circle and the line as one endpoint and the center of c2 as the other endpoint, we can create the base of an isosceles triangle. The intersection point of the perpendicular bisector of this segment and the line is the other vertex of the triangle and the center of the desired circle.
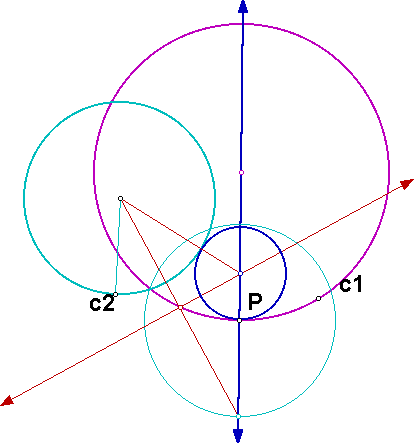
Click here for a GSP sketch of the construction.
The Locus of the Center
If we trace the center of the constructed circle as P moves around the circle c1, we again find that the locus of the center is an ellipse.
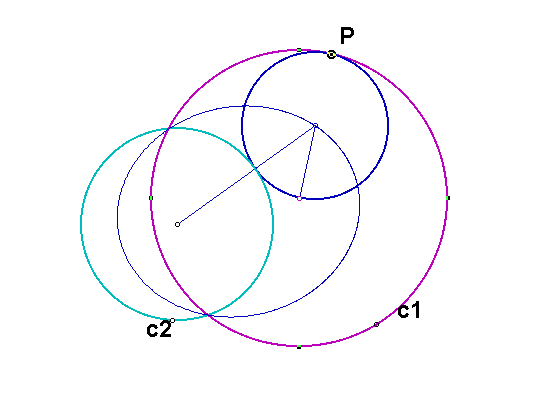
We can construct the segments joining the center of the constructed circle to the centers of the given circles, and we see that the sum of the lengths of these two segments is the same as the sum of the lengths of the radii of the two given circles. Since this sum is constant, the locus is an ellipse. We also see that the ellipse intersects the two circles that the intersection points of the two circles.
Click here for a GSP animation.
Click here for a GSP animation that includes the envelope of tangent lines for the ellipse.
Case 6
Next we will again consider the case where the two circles intersect, but this time we want to construct the circle that is tangent to both circles and either inside both circles or outside both circles. In the diagram below, we want to construct the blue circle.
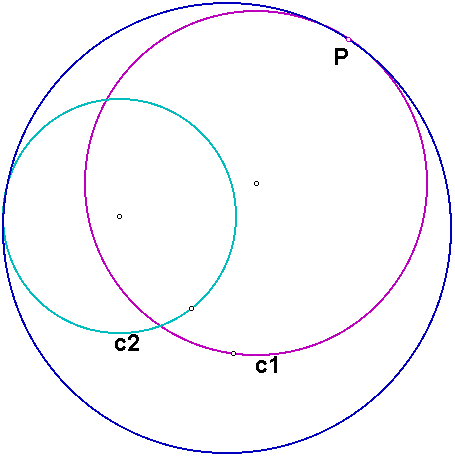
As before, we construct the line through the center of c1 and the point P. Then we construct the circle having center P and the same radius as circle c2.

Again, we want to create the base of an isosceles triangle using an intersection point of this circle and the line as one endpoint and the center of c2 as the other endpoint In this case, the intersection point of the circle and the line that we want to use is the one that is closest to c2. If both points are the same distance to circle c2, we will used the point that is inside c2. Now, the intersection point of the perpendicular bisector of the segment we just constructed and the line is the other vertex of the triangle and the center of the desired circle.
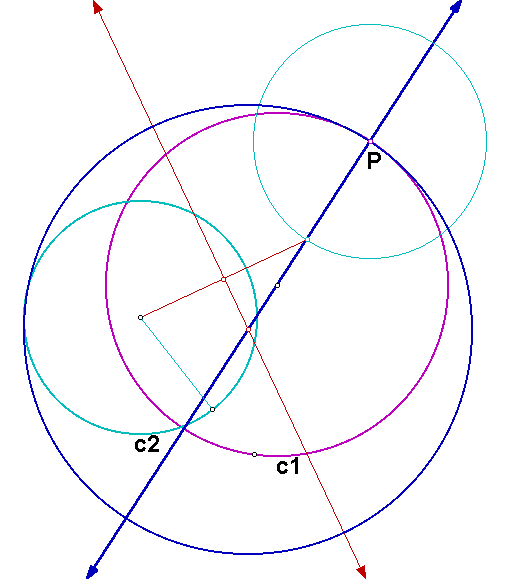
Click here for a GSP sketch of the construction.
The Locus of the Center
If we trace the center of the constructed circle as P moves around the circle c1. In this case, the locus of the center is a hyperbola. If we construct the segments joining the center of the constructed circle to the centers of the two given circles, we see that the difference of the lengths of these two segments is the same as the difference of the lengths of the radii of the two given circles. Since this difference is constant, the locus of the center is a hyperbola.
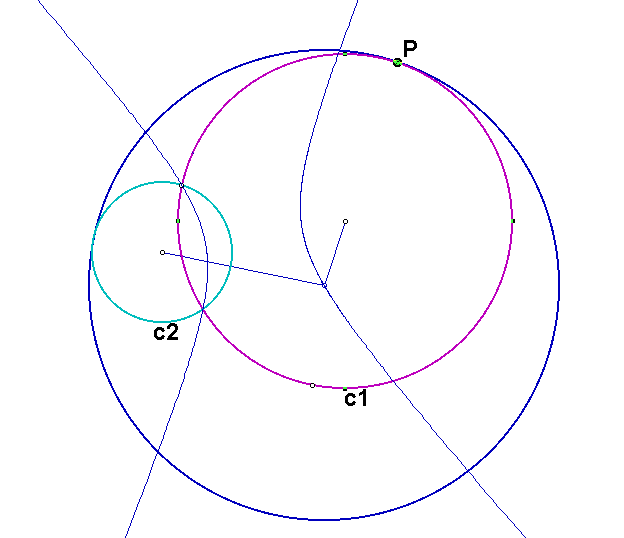
Click here to see a GSP sketch of the animation for the hyperbola.
Click here to see the animation that includes the tangent lines for the hyperbola.
Case 7
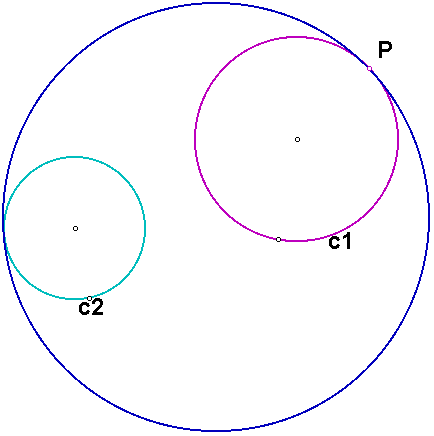
Now let's consider the case when the two given circles are disjoint. First we will construct the circle that is tangent to both circles, and one of the given circles is inside the constructed circle. In the diagram below, we want to construct the blue circle.
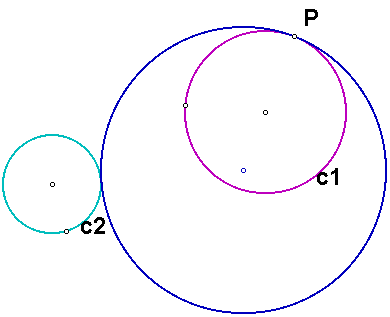
The construction is similar to cases 1, 3, and 5 above. Here is what the construction looks like.
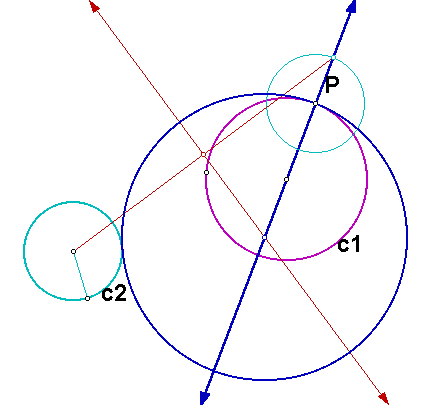
Click here for a GSP sketch of the construction.
The Locus of the Center
If we trace the center of the constructed circle as the point P moves around c1, we see that the locus of the center of the constructed circle is a hyperbola. Why is it a hyperbola?
We can construct the segments joining the center of the constructed circle to the centers of the given circles. We see that the difference of the lengths of these two segments is the same as the sum of the lengths of the radii of the two given circles. Since this sum is constant, the locus of the center of the constructed circle is a hyperbola with foci at the centers of the given circles.
Click here to see a GSP sketch of the animation for the hyperbola.
Click here to see the animation that includes the tangent lines for the hyperbola.
Case 8
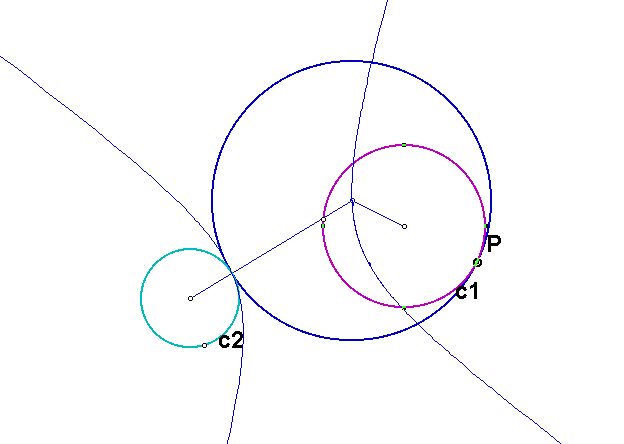
Let's again consider the case when the two given circles are disjoint but let us construct the circle that is tangent to both circles such that the given circles are either both inside or both outside of the constructed circle. In the diagram below, we want to construct the blue circle.
This construction is similar to cases 2, 4, and 6 above. Here is what the construction looks like.
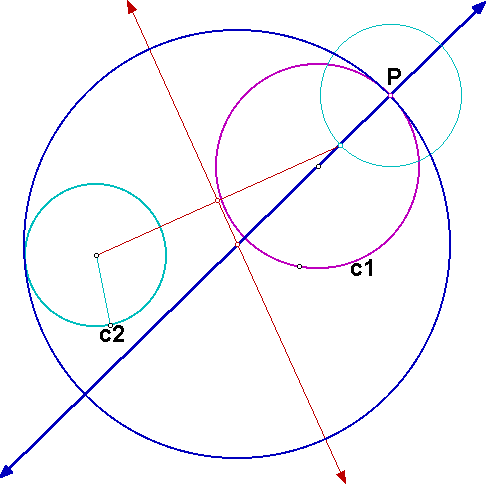
Click here for a GSP sketch of the construction.
The Locus of the Center
If we trace the center of the constructed circle as the point P moves around c1, we see that the locus of the center of the constructed circle is again a hyperbola. Why is it a hyperbola?
We can construct the segments joining the center of the constructed circle to the centers of the given circles. We see that the difference of the lengths of these two segments is the same as the difference of the lengths of the radii of the two given circles. Since this difference is constant, the locus of the center of the constructed circle is a hyperbola with foci at the centers of the given circles.
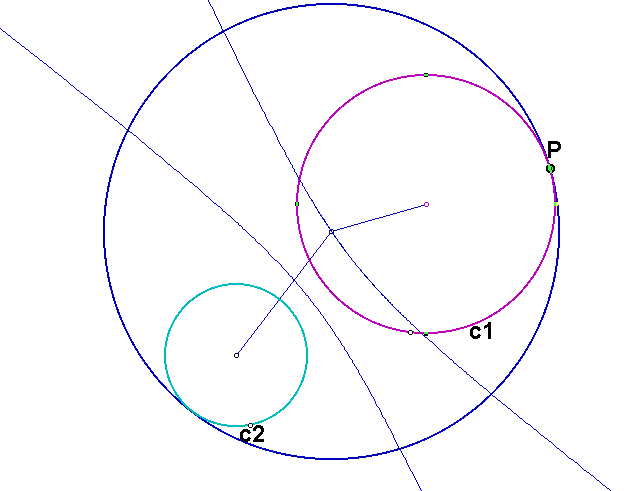
Click here to see a GSP sketch of the animation for the hyperbola.
Click here to see the animation that includes the tangent lines for the hyperbola.
The Locus of the Midpoint of the Base of the Isosceles Triangle
In each case, we constructed an isosceles triangle. Now let's consider the locus of the midpoint of the base of the isosceles triangle. The constructions in cases 1, 3, 5, and 7 were basically the same, and the constructions in cases 2, 4, 6, and 8 were basically the same. Therefore, we will only consider the constructions in case 1 and case 2.
For the construction in case 1, we get the following locus of the midpoint.
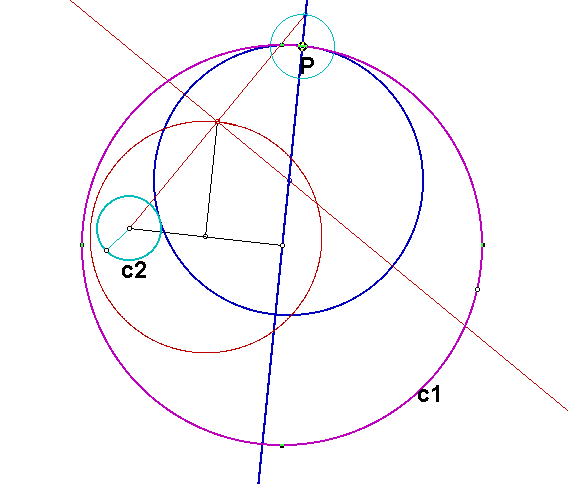
We see that the locus is a circle, and the center of the circle is the midpoint of the segment joining the centers of the two given triangles.
Click here for a GSP sketch of the animation. Move the circles c1 and c2 to explore cases 3, 5, and 7. In all cases, the locus is a circle centered at the midpoint of the segment joining the centers of the two circles.
For the construction in case 2, we get the following construction for the locus of the midpoint.
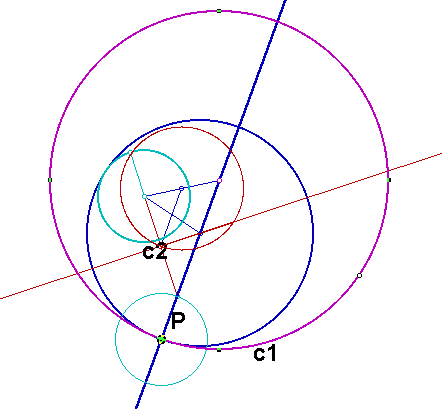
As before, the locus of the midpoint is a circle, and the center of the circle is the midpoint of the segment joining the centers of the given circles.
Click here for a GSP sketch of the animation. Move the circles c1 and c2 to explore cases 4, 6, and 8. In all cases, the locus is a circle centered at the midpoint of the segment joining the centers of the two circles.