

To prove the theorem, we will need the following lemma:
Click here for a proof of the lemma.
When triangle LMN is constructed in the manner described in the statement of the problem, triangle LMN is always acute. Therefore, we can use the lemma in the proof of the theorem, regardless of whether triangle ABC is acute, right, or obtuse.
Construct the circumcenter O of triangle ABC. Construct the segments ON and OM.
From the lemma, we have,
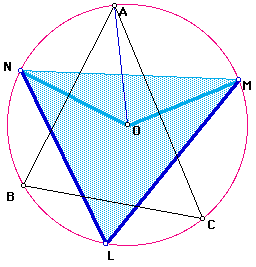
(Click here to verify using GSP.)
Since A is between M and N,
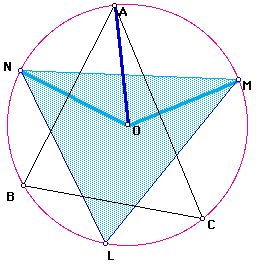
So we now have
Consider the angle MBA. Since M is on the bisector of angle CBA, the measure of angle MBA is half the measure of angle CBA. Since angle CBA is an angle in a triangle, the measure of angle CBA is less than 180 degrees. Therefore, the measure of angle MBA is less than 90 degrees, so it is acute.
Similarly, the measure of angle ACN is half the measure of angle ACB, so the measure of angle ACN is less than 90 degrees.
Since angles MBA and ACN are both acute, we can apply the lemma to them to get
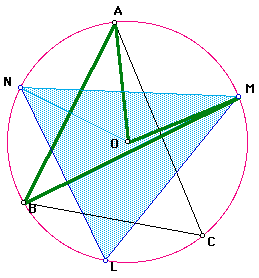
So now we have
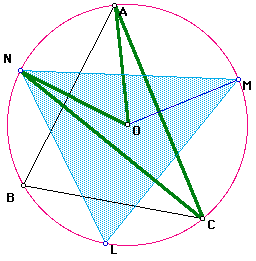
Since M is on the bisector of angle CBA,
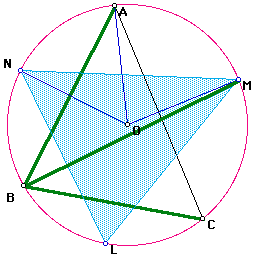
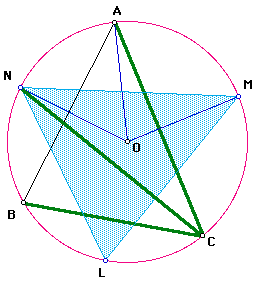
Now we have
Similarly,

This proof does not require that triangle ABC be acute, so the result holds for acute, right, and obtuse triangles.