

![]()
How does changing a, b, and k change the graph? Given a pair of equations of this form, what are the slope and y-intercept of the resulting graph?
Given the coordinates of a point that a line goes through and the slope of the line, can a pair of parametric equations of this line be written?
In NuCalc, the parametric equations are written in the following form:
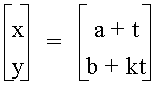
Let's select values for a and b, and overlay graphs for several values of k. Let's let a = 1 and b = 1. We will explore the graphs of the following parametric equations:
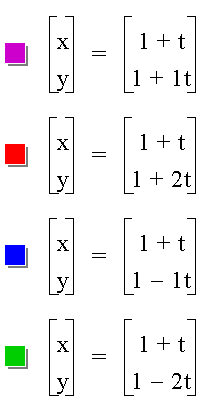
In the first equation, k = 1.
In the second equation, k = 2.
In the third equation, k = -1.
In the fourth equation, k = - 2.
Let's look at the graphs.
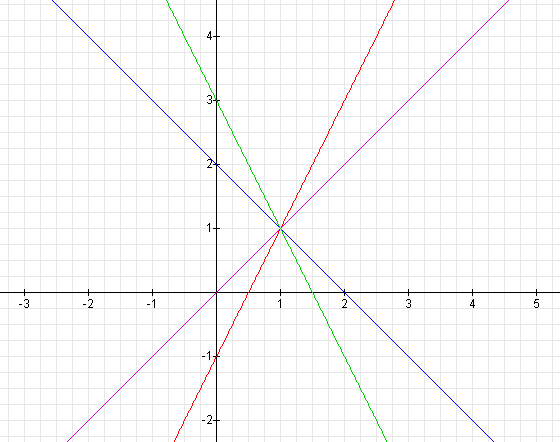
As you can see, when k = 1, the line goes through the points (0,0) and (1,1). Therefore, its slope is 1.
When k = 2, the line goes through the points (0,-1) and (1,1), so its slope is 2.
When k = -1, the line goes through the points (1,1) and (2,0), so its slope is -1.
When k = - 2, the line goes through the points (0,3) and (1,1), so its slope is -2.
In these equations, the slope of the lines are the same as the value for k in the equations
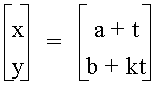
Is this always the case? Let's look at another example. Let's let a = - 2 and b = 4 and look at the graphs of the following equations.
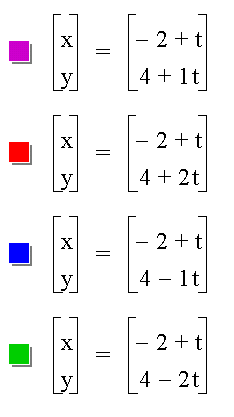
As before, in the first equation, k = 1, and in the second equation, k = 2. In the third equation, k = -1, and in the fourth equation, k = - 2.
The graphs of these equations are the following:
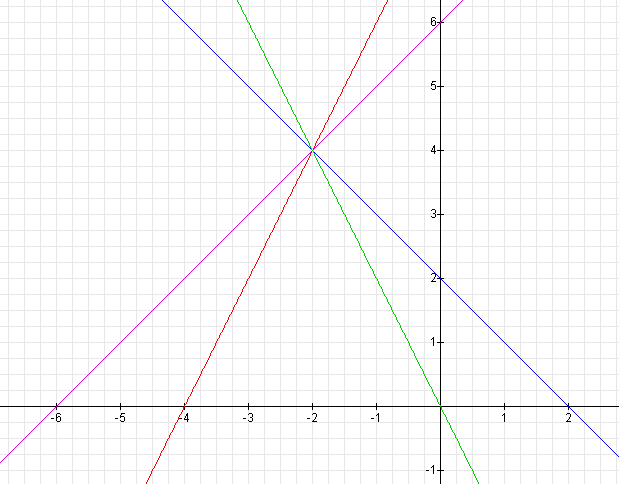
When k = 1, the line goes through the points (-6,0) and (-2,4). Therefore, its slope is 1.
When k = 2, the line goes through the points (-4,0) and (-2,4), so its slope is 2.
When k = -1, the line goes through the points (-2,4) and (0,2), so its slope is -1.
When k = - 2, the line goes through the points (-2,4) and (0,0), so its slope is -2.
As before, the value for k in the parametric equations
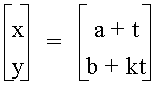
determines the slope of the line.
Why does k determine the slope,
and how do a and b affect the graphs?
Let's go back to the original equations:
![]()
and
![]()
Solving both equations for t yields
![]()
and
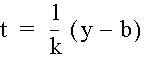
Setting these two equations for t equal to each other, we see
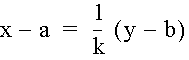
Solving for y, we get
![]()
or
![]()
Thus, we see that k is indeed the slope of the graph of the equations
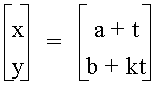
We also see that the y-intercept of the equation is given by b - ka.
Let's try a few examples.
What does the graph of
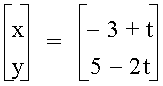
look like? In this example, a = - 3, b = 5, and k = - 2. Therefore, we expect the graph to be a line with slope k = - 2 and y-intercept b - ka = 5 - (- 2)(- 3) = - 1.
Here is the graph:
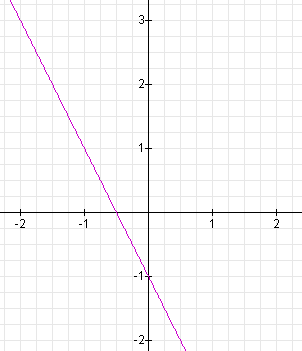
As we expected, the slope of the line is - 2, and the y-intercept is -1.
The graph of
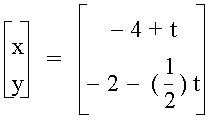
will have a slope of - (1/2) and y-intercept of - 4.
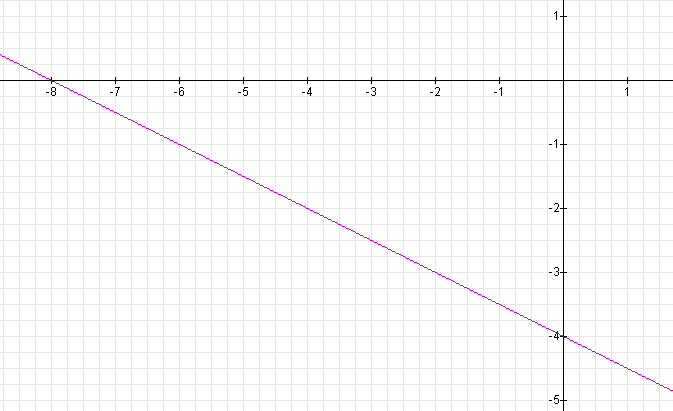
The graph of
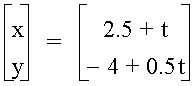
will have a slope of 0.5 and a y-intercept of -5.25.
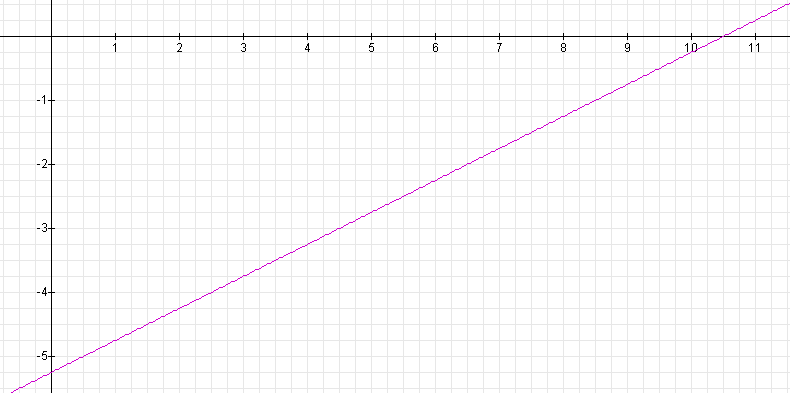
Given the coordinates of a point that a line goes through and the slope of that line, what are the parametric equations of the line?
For example, let us write the parametric equations of a line through (7,5) with a slope of 3. Since the slope of the line is 3, we know that k = 3. Now we need to find a and b. We know that the equation
![]()
describes the line. Since the point (7,5) is on the line, we know that
![]()
or
![]()
We can choose any values for a and b as long as they satisfy the above equation. Let's let a = 0 and b = - 16. Then the parametric equations of the line are
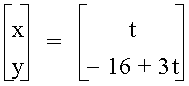
The graph of this parametric equation is
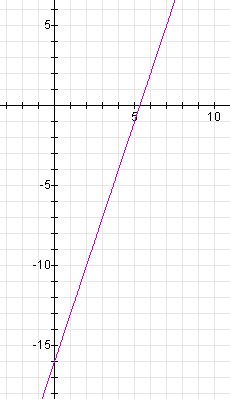
As you can see, the line goes through the point (7,5) and its slope is 3.
We did not have to choose a = 0 and b = - 16. We could have let a = 1 and b = - 13, or a = - 1 and b = - 19. We can choose any values for a and b as long as they satisfy
![]()
Conclusion
Parametric equations of the form
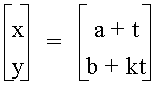
describe a line
![]()
with slope k and y-intercept b - ka.