In this paper, we consider a locus of points in the plane determined by some relation to two fixed points. The word locus(plural loci) is Latin and translates into English as place. So if we say we are looking for the locus of points in a plane that are 5 units from the origin, we are just saying we want to find all the places that are 5 units away from the origin and describe what they look like as a group. We say  the locus of points in a plane 5 units from the origin is a circle with radius 5 centered at the origin. The phrase in a plane is important, since without that restriction, (i.e. allowing points in space) we would be describing a sphere with radius 5 centered at the origin.

For example, consider points A(-3 , 0) and B(3 , 0) on a Cartesian coordinate system. What is the locus of points in the plane equidistant from A and B? We picture points A and B and try to imagine placing points on the page that are the same distance from point A as they are from point B.

The result is a collection of points on a line that is the perpendicular bisector of segment AB. In our specific case, the locus is the y-axis.

Given fixed points (a,b) and (c,d) we seek all points (x,y) such that

where k is some chosen constant.

For (a,b) = (-3,0) and (c,d) = (3,0) we obtain the graph shown below. Click on the graph to open Graphing Calculator and explore for various values of k, or click here to see a Quicktime movie as k varies from 6 to 20 in steps of  0.1.
 
 

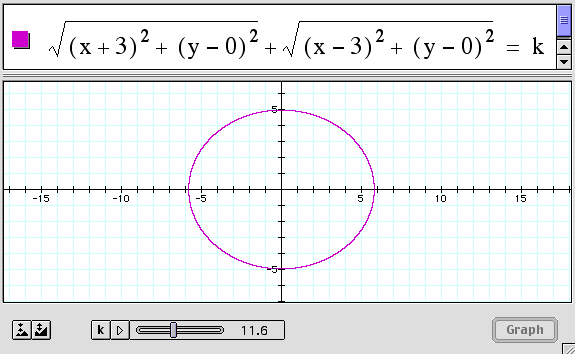
So the locus of points in a plane chosen so that the sum of the distances to two given points is constant is an ellipse, as we suspected since this is the locus definition of ellipse. The given points are the foci of the ellipse.

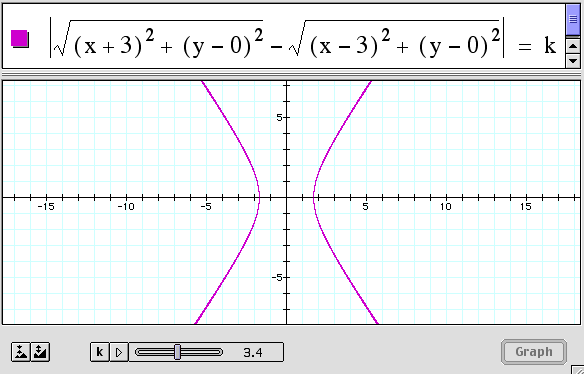
We started with the locus definition of a hyperbola, and as you can see, the locus of points appears to be  a hyperbola and the two given points are the foci.

So far, our discussions have not really deviated from the typical high school curriculum. But what if we ask for the locus of points in a plane such that the product of the distances to two fixed points is a constant? Simply changing the addition or subtraction to a multiplication in one of the above investigations gives an immediate visual response to our question. As before click anywhere on the graph to open Graphing Calculator, or click here to see a Quicktime movie as k varies from 0 to 40 in steps of .05.

This investigation is easily within the grasp of a high school student, who should be asked to find the value of k for which the graph degenerates into two pieces and to explore algebraically why it happens.

It is interesting to think of the graph for each value of k as a slice of a three-dimensional figure. Click here to see a Quicktime movie or here to open Graphing Calculator and explore this 3-D graph.

Suggested topics for Web research are lemniscates and ovals of Cassini.

Of course, any of these figures may be rotated by selecting the fixed points not on the axes - another topic that often gets little attention in high school mathematics, but is easily accomplished with graphing software.

 

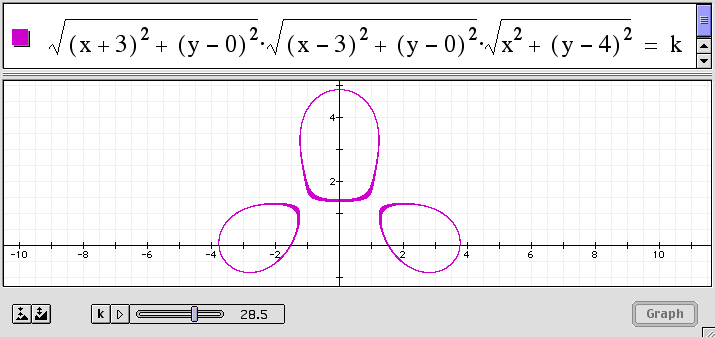
When I started this web page, I considered including the question What is the locus of points in a plane such that the ratio of the distances to two fixed points is a constant?, but I didn't think it was very interesting since it was obvious the locus was a circle. Then in the December, 2001 issue of The Mathematics Teacher(p 738) the following letter appears in Reader Reflections:

Click here to see my proof. To see this locus definition of circle implemented in GSP, click here.

The title of this write-up "Stuck in loci again" is a play on a lyric from a Credence Clearwater Revival song called Lodi.