For any triangle, several sets of segments are concurrent: the perpendicular bisectors of the sides, the angle bisectors, the altitudes, and the medians. This paper briefly presents proofs of theses four claims.

Theorem 1: The perpendicular bisectors of the sides of any triangle are concurrent.

The proof makes use of the following figure. Click anywhere on the figure to open Geometer's Sketchpad and explore.

Line MC and line LC are the perpendicular bisectors of sides YZ and XZ, respectively.

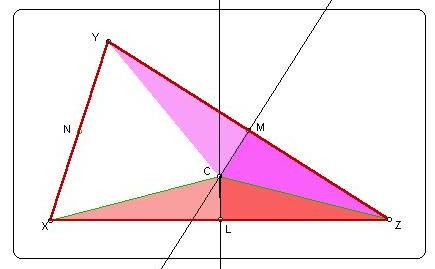
Proof: Let XYZ be any triangle and points L, M, and N be the midpoints of the sides as shown in the figure above.Construct lines perpendicular to XZ at L and to YZ at M. These lines cannot be parallel, for that would imply that segments XZ and YZ were collinear. Call the intersection point C, as shown above.
         Triangles CLX and CLZ are congruent by the SAS congruence theorem so that CX = CZ.
Also, triangles CLZ and CMY are congruent by the SAS congruence theorem so that CZ = CY.
We must conclude that CX = CY, making triangle CXY isosceles. Then CN is not only a median of triangle CXY, but also the perpendicular bisector of XY.
         Hence, all three perpendicular bisectors of the sides of  triangle XYZ are concurrent at point C.

The proof is exactly the same if triangle XYZ is obtuse, causing point C to lie outside the triangle. You can explore this case in GSP by clicking on the figure above.

We get an added bonus by noting that point C is equidistant from X, Y, and Z. making C be the center of a circle through the vertices of the triangle. So we have a way to find the center of any circle: pick any three points on the circle and create the perpendicular bisectors of the segments that they determine. Click here to explore for yourself or here to run a script to demonstrate.

Theorem 2: The angle bisectors in any triangle are concurrent.

The proof makes use  of the following figure. Click anywhere on it to open Geometer's Sketchpad and explore.

In triangle ABC, AI and Bi are angle bisectors. Segments IE, IF, and IG are perpendicular to their respective sides of the triangle.

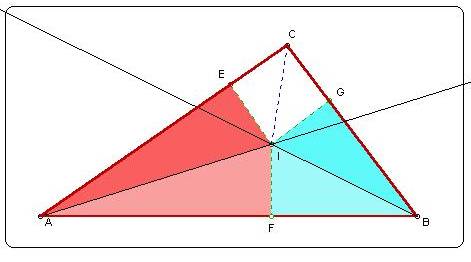
Proof:  Let  ABC be any triangle and construct angle bisectors for angles A and B. These rays must intersect at some point I as shown above. From I, construct perpendiculars to the sides of the triangle, forming right triangles AIE, AIF , BIF, and BIG .
        Triangles AIE and AIF are congruent by the AAS congruence theorem, so that IE = IF.
Also, triangles BIF and BIG are congruent by the AAS congruence theorem, so that IF = IG.
We must conclude that IE = IG, making triangles CIE and CIG congruent by the hypotenuse-leg congruence theorem.Then angles ICE and ICG are congruent, implying that segment IC lies on the angle bisector of angle C and that all three angle bisectors are concurrent at point I.

We get an added bonus in that point I must be the center of a circle (with radius IE = IF = IG) that is inscribed in triangle ABC. Click here for a GSP script to draw an inscribed circle in any triangle.

Theorem 3: The altitudes in any triangle are concurrent.

The proof makes use of the following figure. Click anywhere on it to open Geometer's Sketchpad and explore.

In triangle ABC, two altitudes are shown in green. For point A=(a,0), a is shown as a negative number, but A could be anywhere on the x-axis, as you can see by clicking on the figure to open GSP and relocating point A.

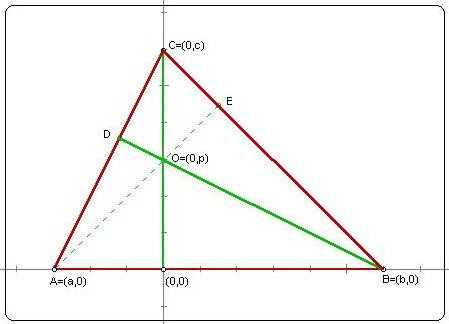
 Proof: Locate any triangle ABC so that side AB lies along the x-axis and the altitude from C lies along the y-axis as shown above. The altitude from B must intersect the altitude from C at some point with coordinates (0,p). Since BD is perpendicualr to AC, the slope of BD is the negative reciprocal of the slope of AC, so -p/b = a/c and b = (-pc)/a
If AE is the altitude from A and hence perpendicular to BC, then the slope of AE must be b/c . Substituting for b shows the slope of AE to be -p/a, implying that AE must pass through point (0,p).
Thus, all three of the altitudes of triangle ABC are concurrent at O, a point called the orthocenter of ABC.

Theorem 4: The medians of any triangle are concurrent.

The proof makes use of the following figures. Click anywhere on the figure to open Geometer's SketchPad and explore.

Two views of triangle ABC, with points D, E, and F as midpoints of the sides.

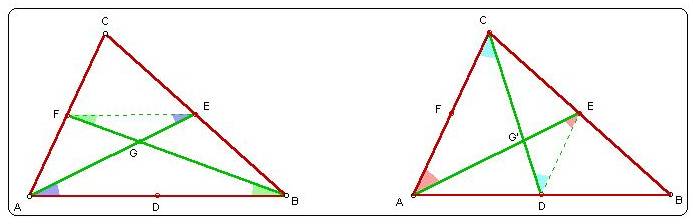
Proof: In any triangle ABC, construct the midpoints D, E, and F of the sides as shown in the left figure above. Since EF is parallel to AB, the green angles in the figure are congruent and the blue angles are congruent, making triangles ABG and FEG similar.
Also, FE = .5 AB, so point G is located so that EG =  .5  AG.
In the figure to the right above, an analagous argument leads to the conclusions that triangles ACG' and  EDG' are similar. The big question is - are points G and G' really the same point?
Since ED = .5 AC, it must be true from similar triangles, that EG' = .5 AG'. There is only one point on AE where that is true, so G = G'.
Thus, the three medians of triangle ABC are concurrent at point G.

Return to D Hembree's EMAT 6680 page
email to : dhembree@coe.uga.edu