
Hinged Tessellations
by
D. Hembree
This page displays some common regular and semi-regular
tessellations, but with a twist. The polygons are hinged at one
or more vertices so that the appearance of the tessellation may
be changed dynamically. All implementations are done in Geometer's
Sketchpad and can be explored by clicking on the figure. This
could be a fun extension of the study of tessellations in middle
or secondary mathematics.
As a first example, consider a tessellation of squares as shown:

Each blue square is hinged at its vertices so that the tessellation
changes as any blue square is rotated and my look like one of
the following:


The blue squares have only rotated, but the yellow
squares have become rhombi. Watching the transformation is fascinating
and I suggest you take the time to watch it in GSP. Clicking on
any of the figures will take you there (if you have GSP on your
computer).
Here's my aborted attemp to make a hinged tessellation
with triangles:
 As you can see, it's no longer a tessellation (and
some of the triangles were incorrectly placed), but you can still
open the GSP file and see it rotate.
As you can see, it's no longer a tessellation (and
some of the triangles were incorrectly placed), but you can still
open the GSP file and see it rotate.
I had better luck with hexagons, as the next figure shows:
 Only the green hexagons are "stable". Try
it and see!
Only the green hexagons are "stable". Try
it and see!
Here are hexagons again, but with triangles and squares:
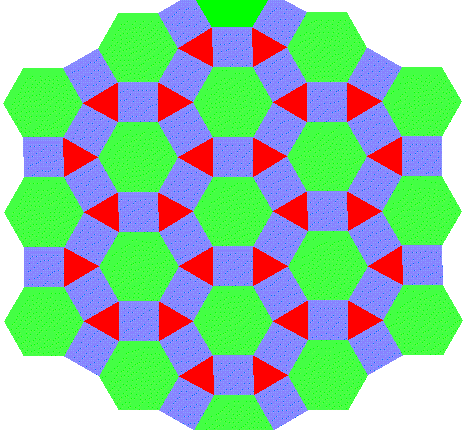 Again, only the green hexagons are "stable".
Again, only the green hexagons are "stable".
This looks like a traditional quilt pattern, but it "morphs"
into other patterns while maintaining a beautiful symmetry.
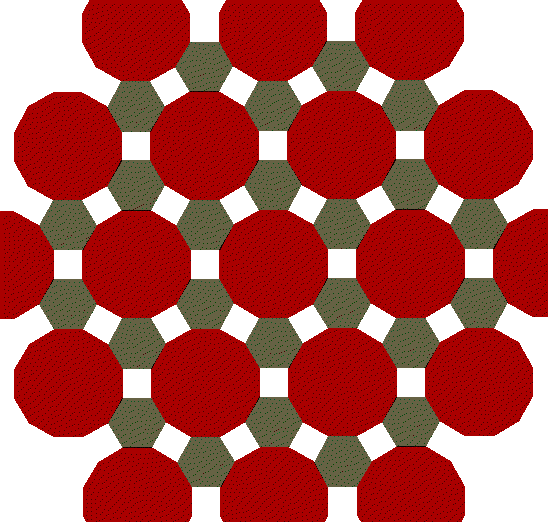
This traditional tile pattern is composed of octagons and
squares, but the squares transform into beautiful stars and pinwheels.

The octagons rotate, adding triangles to the squares
and then collapsing into a single octagon.
The final hinged tessellation here
is composed of dodecagons, hexagons, and squares. Compare
the changing patterns of the squares to the tessellation above.
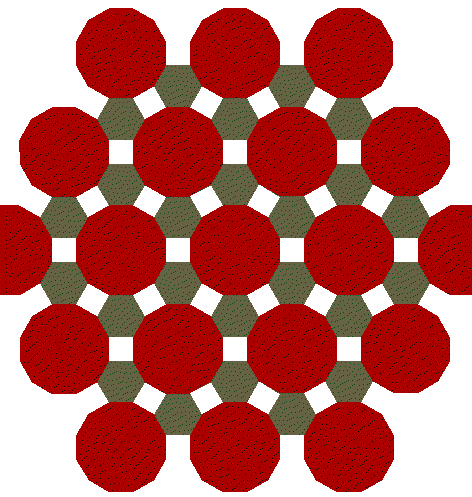
Compare the above tesselation to this one, which appears
the same, but has "stable" squares which rotate with
the dodecagons.
My final attempt was not a tessellation, but a hinged dissection
puzzle of an equilateral triangle into a square by Dudeney.
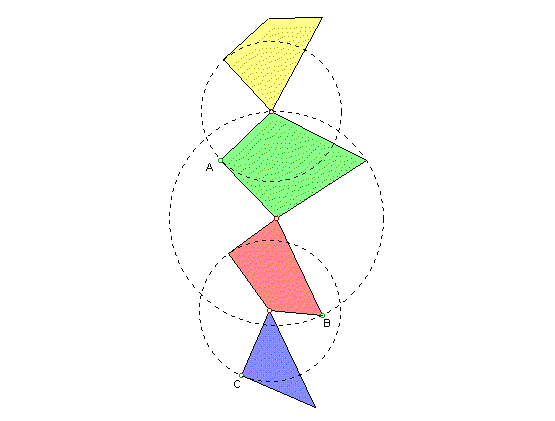 Click to open GSP and try the puzzle
Click to open GSP and try the puzzle
Return to D. Hembree's EMAT
6680 page
Email to dhembree@coe.uga.edu









