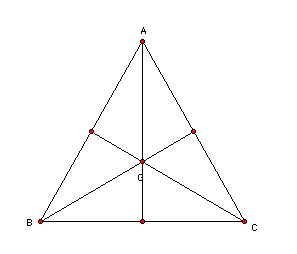
Let's look at the centroid of a triangle. The centroid of a triangle is the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite.

Let's explore its location for various shapes of triangles.

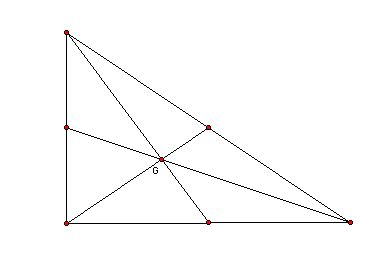
Right triangle.

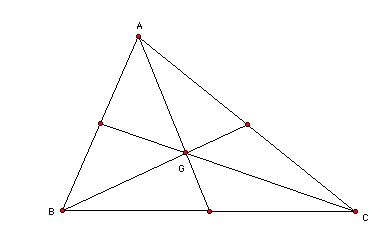
Acute triangle.

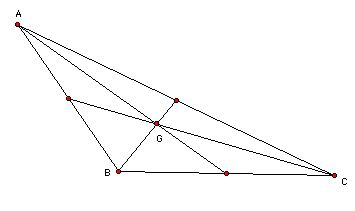
Obtuse triangle.

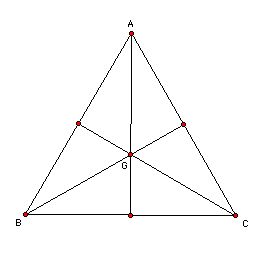
Equilateral triangle.

Isosceles triangles.

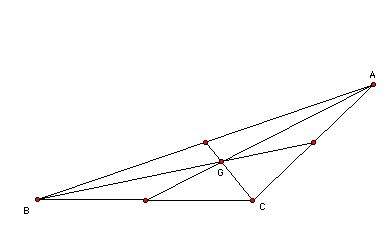
Scalene triangle( Any triangle that is not an isosceles triangle )

 
 
 

In properties of the centroid of a triangle, we can check two properties.
First, if we rable the mid-point of segment BC as D, we can check AG: GD= 2: 1
Second, the areas of the trangles GAB, GAC, adn GBC are  the same and also the areas of the triangls GBD and GDC are the same.
You can check these facts and explore the locations of a centroid (G) for various shapes of triangles by using Geometer's Sketchpad (GSP)

 You can explore the locations of a orthocenter (H) for various shapes of triangles by using Geometer's Sketchpad (GSP)

 You can explore the locations of a circumcenter (C) for various shapes of triangles by using Geometer's Sketchpad(GSP)

 You can explore the locations of a incenter ( I ) for various shapes of triangles by using Geometer's Sketchpad(GSP)

 You can explore the relationships among G, H, C, and I for various shapes of triangles by using Geometer's Sketchpad(GSP)

Return to the Top