Introduction:  Let's look at the relationship between a triangle and its medians.

Let's find some relationship between the two triangles.

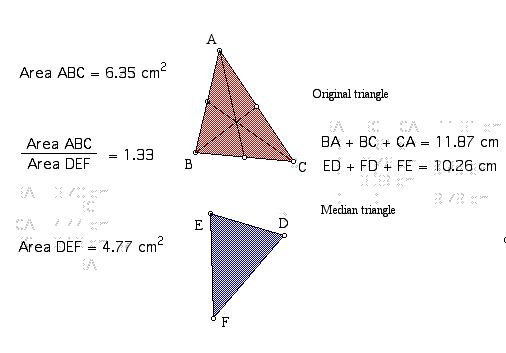
First, let's compare the areas of the two triangles.

Their areas and perimeters are not equal.

The ratio of the areas is the same but the ratio of the perimeters is different.

Although we change the lengths of the orginal triangle, there is no change in the ratio between the two triangles.

The ratio is 1.33

If you want to check these facts, click here.

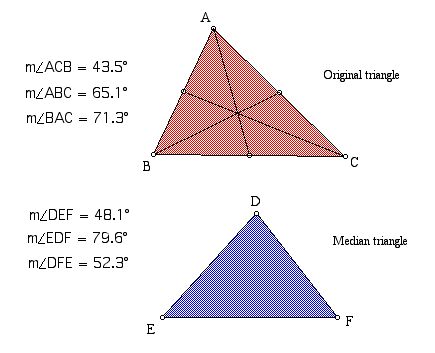
The two triangles are neither  congruent  nor similar.

Let's try to prove that the ratio of the areas is 1.33

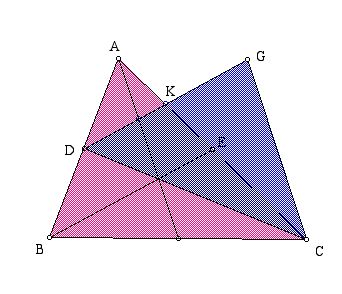
Proof : ABC is the orginal triangle  and CDG is a median triangle

           Since DK = 1 / 2 * BE and BE  = DG,

           ( the area of the triangle ACD ) = 1 / 2 * ( the area of the triangle ABC )

            and  ( the area of the triangle CDK ) = 1 / 2 * ( the area of the triangle CDG ).

            Since AD = 1 / 2 * AB and EK = 1/ 2 AE,

             ( the area of the triangle CDK ) = 3 / 4 * ( the area of the triangle ACD )

            Since triangle ACD is the half of the triangle ABC and the triangle CDK is the half of the triangle CDG,

            We can conclude that (the area of the triangle ABC) / ( the area of the triangle CCG) = 1.33.
 

Return to the Top