Problem: Given two circles and a point on one of the circles.
             Construct a circle tangent to the two circles with one point of tangency being the designated point.

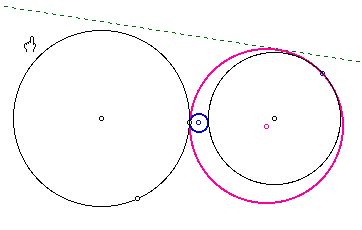
This is my construction of the tangent circles.

You can check my scripts to construct the tangent circle to two given circles if you would click here.

T;he loci of the centers of the tangent circles for all case I construct.

When the two given circles intersect, the locus of the centers of the constructed tangent circles looks like this.

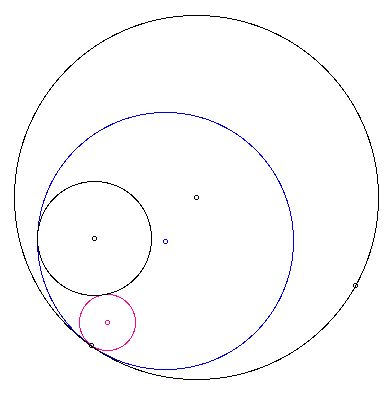
When the two given circles are disjoint, the locus of the centers of the constructed tangent circles looks like this.

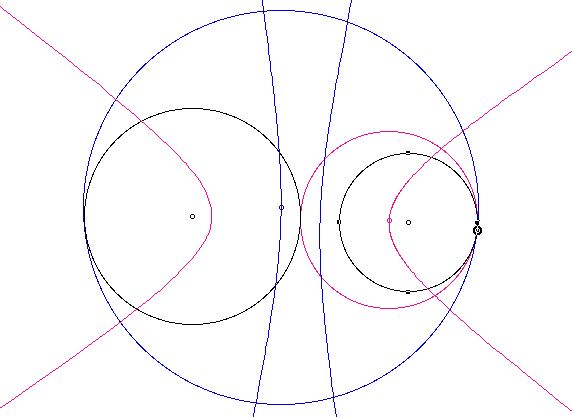
If you want to check the above facts, you can check those in the GSP by clinking here.

Discussion

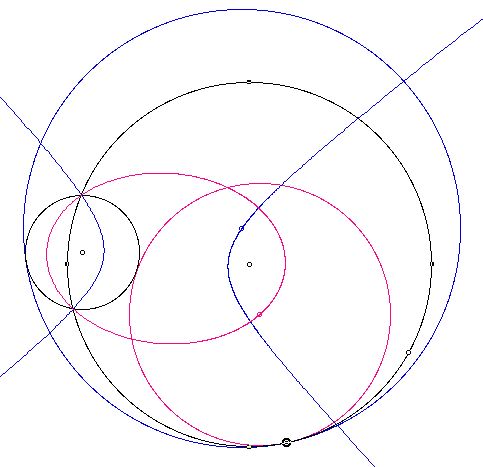
Let's construct tangent circles if the two given circles intersect.

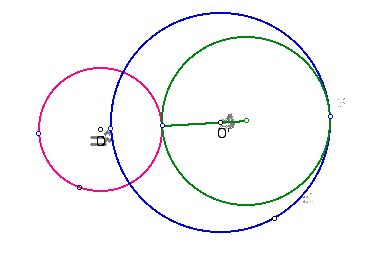
If the circle O and the circle O' are intersect, first we need to consider the line passing through O and O'.

Next, we can find two intersection point with O and O' and then we can find the green circle easily.

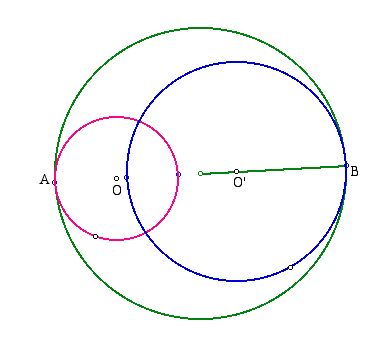
Similarly, if you want to find the external tangent circle, we need to consider the line passing through O and O'.

Then we need to find the intersection points A and B and find midpoint of the segment of A and B.

And then find the circle centered at  the midpoint with the radius of  the distance from the midpoint to B.

Examination

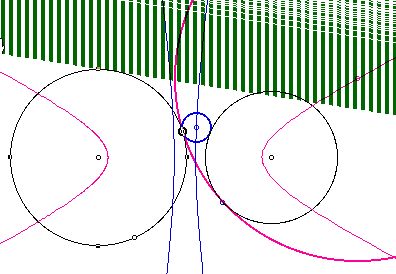
Let's examine the trace of the tangent line in each case.

First, when one circle is incide the other.

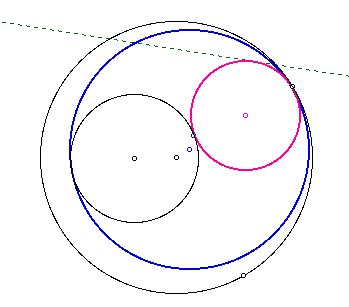
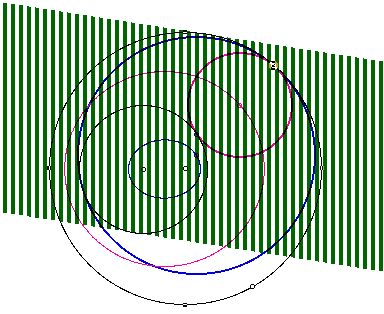
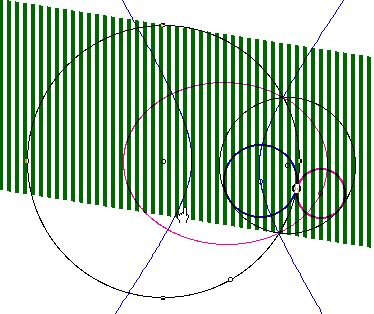
Second, when the two given circles intersect.

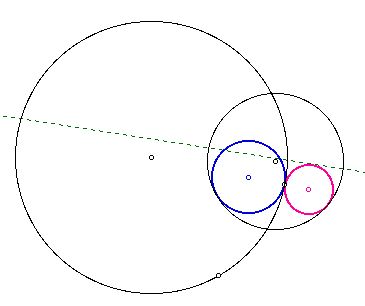
Third, when the two given circles are disjoint.