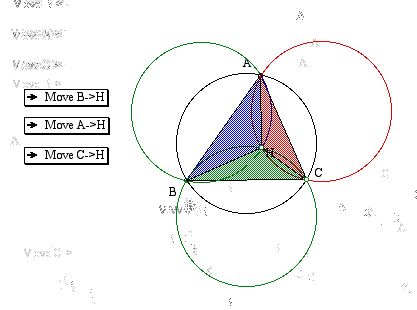
If any vertex of the triangle ABC is moved to where the orthocenter H is located, H is located at the location of the vertex.
The vertex of each triangle HAB, HBC, and HAC is C, A, and B respectively.

Click HERE for a GSP file with "move" buttons to see these animations.
Orthocenter H and intersections with the three altitudes.
After constructing any acute triangle ABC and it's circumcircle, let's consider the three altitudes AD, BE, and CF.
Extend each altitude to its intersection with the circumcenter at corresponding points P, Q, and R.
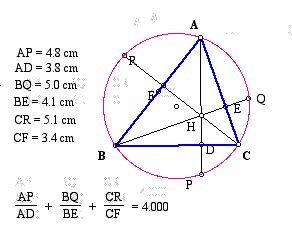
Click HERE for a GSP sketch.
Proof: The area of triangle ABC equals 1/2 * AD * BC = 1/2 * BE * AC = 1/2 * AB * CF ....... (1).
Since the area of triangle ABC equals to the sum of three triangls ABH, BCH, and ACH,
we can get the equation 1/2 * AD * BC = 1/2 * ( HD * BC + HE * AC + HF * AB ).
If we would divide both sides with 1/2 * AD * BC,
we can get 1 = HD/ AD + ( HE * AC) / ( AD * BC ) + (HF * AB) / ( AD * BC ).
Because of AD * BC = BE * AC = AB * CF, we can get the equation
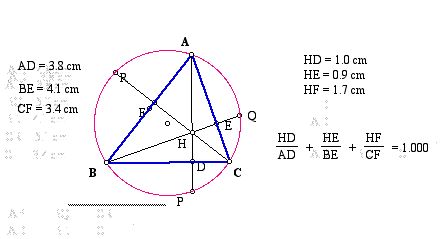
1 = HD / AD + HE / BE + HF / CF.
Proof: From
the equation 1 = HD / AD + HE / BE + HF / CF.
we can get 2 = 3 - 1 = 3 - ( HD / AD + HE / BE + HF / CF )
= 1 + 1 + 1 - ( HD / AD + HE / BE + HF / CF ).
= AD / AD + BE / BE + CF / CF - ( HD / AD + HE / BE + HF / CF ).
= ( AD - HD ) / AD + ( BE - HE ) / BE + ( CF - HF ) / CF
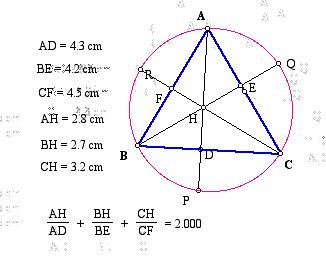
= AH / AD + BH / BE + CH / CF.
So, we can get the the equation ( AH / AD + BH / BE + CH /
CF ) = 2.