Explorations of x=cos(at), y=sin(bt).
For various a and b, let's investigate x=cos(at), y=sin(bt) for 0 <
t < 2 ![]() .
.
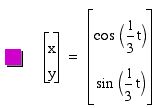
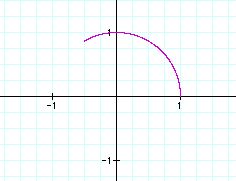
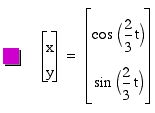
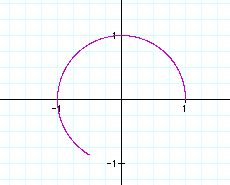
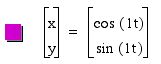
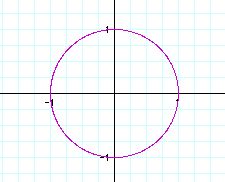
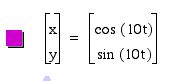
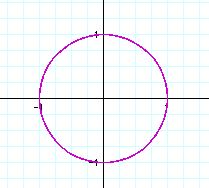
We can easily guess that if a and b are equal, a and b are related
with the period of the circle with radius 1.
After fixing a value, let's change b value.
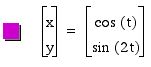
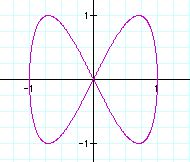
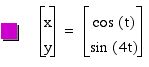
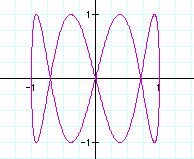
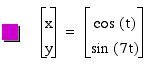
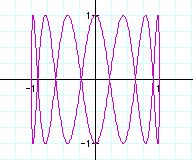
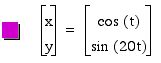
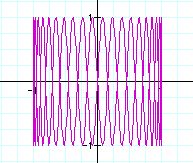
From the graphs, we can guess the role of b value.
After fixing b value, let's change a value.
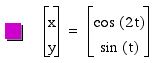
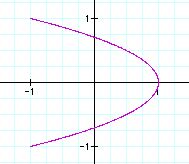
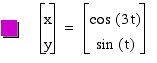
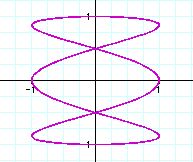
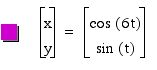
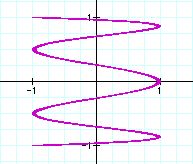
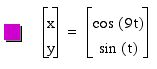
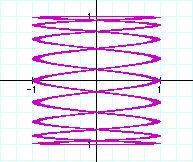
Similarly, we can guess the role of a value from the graphs.
Exporations of x=(1-t^2)/(1+t^2), y= 2t/(1+t^2).
Let's explore the graphs of
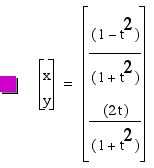 for
-
for
-![]() < t <
< t < ![]()
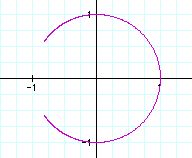
If we would change the domain of t,
for -3![]() < t <
< t < ![]()
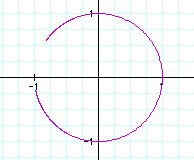
for -![]() < t < 3
< t < 3![]()

As the domain increase, the ends of the circle approaches point ( -1,0
).