The Spreadsheet in Mathematics Explorations.
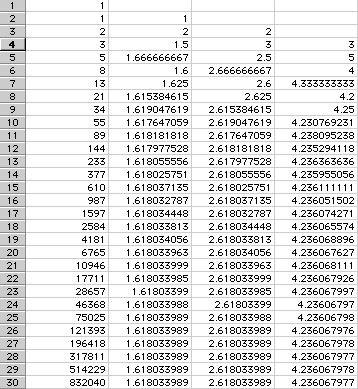
Problem: Generate a Fibonnaci sequence in the first column using f(0)=1, f(1)=1, f(n) = f(n-1) + f(n-2)
Let's look at the Fibonnaci sequence and the ratio of each pair of adjacent
terms
Seq. Fibonnaci The ratio Second Third

Let's look at the graph of a Fibonnaci sequence and the ratios of adjacent terms, every second term, and every third term.
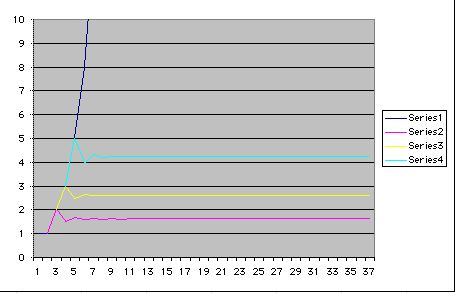
The ratio of each pair of adjacent terms in the Fibonnaci sequence is 1.618033989 and the ratio of every second term is 2.618033989
and the ratio of every third term is 4.236067977.
If you want to check the Excel, click HERE
Lucas Sequence
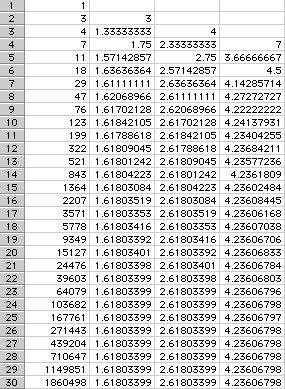
Let's look at a Lucas Sequence f(0)=1, f(1)=3, f(n) = f(n-1) + f(n-2).
Seq. Lucas Ratio Second Third
Let's look at the graph of a Lucas sequence and the ratios of adjacent terms, every second term, and every third term.
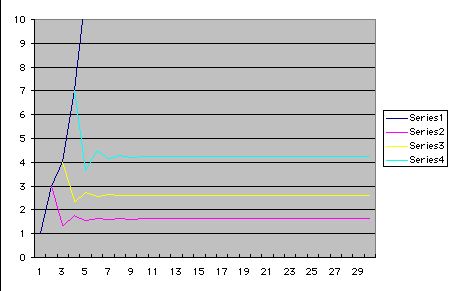
Although the ratio of each pair of adjacent terms in the Lucas sequence is different at several terms with the Fibonnaci sequence, it's the same in the long run.
Similarly, the ratio of every second and third term is the same in the long run between the Lucas sequence and the Fibonnaci sequence.
If you want to check the Excel, click Here