

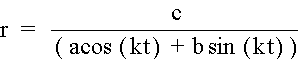
From the graphs, we can see that each of the graphs has a circular shape. The first graph, when a=1, is the purple one. As a changes from 1 to 4, the graph becomes larger, but the shape stays the same. Also, each graph intersects the coordinate system at the origin. Each of the circles seems to have its center point on the y-axis. Therefore, the graphs have the same shape and a common point. Next, we will look at the effect that varying k will have on the graph of the equation.
In the second set of graphs, k was varied from 1 to 4 and set a=1. ]
KEY: k=1 Purple k=2 Red k=3 Blue k=4 Green As k is varied from 1 to 4, the shape of the graph does change. We will also see a pattern emerge from the graph. When k=1, we have a circular shape that is like the graphs in the first set of equations, but the rest of the graphs are a different shape. The next equation, where k=2, forms 4 curves that are shaped similar to the petals of a flower. When k=3, we also have petal shaped curves, but this time we have exactly three petals. In the graph of k=4, we have 8 petal shaped curves.
We can now find the pattern for the graph of the equation when k is varied. When k is equal to an odd number, you have the same number of "petals" as k. When k is equal to an even number, the number of "petals" is twice k. We can check to make sure our pattern holds by trying k=5 and k=6. Look at the graph below to see what the graph looks like.
k=5 k=6 As you can see from the graphs above, the pattern does continue for k=5 and k=6. Therefore, we can surmise that this pattern will continue for any k when a is equal to 1.
Part 2 Graphs of the polar equation given below when a and k are varied. In the first set of graphs, a has been varied from 1 to 3 and k=1. Key: a=1 Purple a=2 Red a=3 Blue In this set of graphs as a is varied from 1 to 3, the shape remains the same. The graph is in the shape of a circle, just like they were in the first graph on this assignment. The circular shape also gets larger as k increases. If we compare this graph to the graph of the first equation where k was varied, it is the same graph. In the first equation we used sin( ) instead of cos( ). The difference is that this graph is centered around the right side of the x-axis, where the first equation was centered around the upper half of the y-axis. Next we will look at what happens in this equation when k is varied.
In this graph, k is varied from 1 to 4 and a=1. Key: k=1 Purple k=2 Red k=3 Blue k=4 Green In this set of graphs as k is varied from 1 to 4, the shape of the graph does change. In the first graph, where k=1, the graph has a circular shape. In the next three graphs, where k=2,3,4, the graph is a "petal" shaped graph with 4,3, 8 "petals", consecutively. This graph is also very similar to the second graph where we used sin( ) instead of cos( ). This graph has been shifted around to be centered around the x-axis, where the sin( ) graph was centered around the y-axis.
Therefore, we can surmise that the sin( ) and cos( ) graphs in these polar equations will have the same shape. The difference between the two graphs is where they are centered around. The sin( ) graph is centered around the y-axis, and the cos( ) is centered around the x-axis.
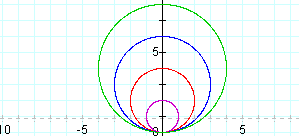
Part 3 Graphs of the polar equation given below with a, k, and b varied. In the first graph, a is varied from 1 to 4 and b and c is set equal to 1. Key: k=1 Purple k=2 Red k=3 Blue k=4 Green As a varies from 1 to 4, the graph has the same shape but the size increases. The first graph, where k=1, is purple. The shape of the graph is circular with a curve in the middle. In the next three graphs, where a varies from 2 to 4 has the same shape. The graph get larger as a increases from 2 to 4.
In the second graph, k is set equal to 1,2,3,1.5,and -1, and a and b are set equal to 1. Key: k=1 Purple k=2 Red k=3 Blue k=1.5 Green k=-1 Pink As k is varied in these graphs, the shape of the graph changes. In the first equation, where k=1, we have a circular shape with a curve in the middle that is centered around the y-axis. When k=2, the shape changes to two large "petal" shaped curves and two small "petal" shaped curves that are centered between the x and y-axis. When k=3, we also have a "petal" shaped curve, this time with three large "petals" and three smaller "petals". When k=1.5, the graph looks similar to k=1, but has only one small "petal" and the two larger "petals" are tilted toward each other, instead of being perfectly symmetrical, as in k=1. When k=-1, the graph has the same shape as k=1. Instead of being centered around the top of the y-axis is has been flipped upside down onto the lower half of the y-axis.
Therefore, we can surmise that in this set of equations k is equal to the number of larger and smaller "petal" curves when k is an integer. We can also say that when k is negative the shape will be the same as when it is positive, but the graph will be shifted in the opposite direction.
In the last graph of this equation, b is set equal to 1,2,3,1.5,0 and a and k are set equal to 1. Key: b=1 Purple b=2 Red b=3 Blue b=1.5 Blue b=0 Light Blue As b varies from 1 to 3, the shape of the graph basically stays the same. The graph is kind of heart shaped with a curve in the middle. The curve of the graph gets smaller and the graph becomes more circular. When b=1.5, the graph gets even more circular and the curve in the middle is gone altogether. When b=0, the graph becomes a circle. Therefore, we can see from the graph that b does effect the shape of the graph, but not as drastically as k does. All of these graphs are also centered around the y-axis, which is the same as the first graph of the equation where a was varied.
Part 4 Graphs of the polar equation given below where a, k, and b are varied. In the first set of graphs a is set equal to 1,2,3,-1 and k and b are set equal to 1. Key: a=1 Purple a=2 Red a=3 Blue a=-1 Green As a is varied, the shape of the graph stays the same but gets larger as a increases. When a=-1 the graph is flipped to the left side of the x-axis, but has the same size and shape as a=1. We can also compare this graph to the earlier graph of sin( ) where a was varied. You can tell that the graphs have the exact same shape, but the graph has been shifted here to center around the x-axis.
In the next set of graphs k is set equal to 1,2,3,4,1.5 and a and b are set equal to 1. Key: k=1 Purple k=2 Red k=3 Blue k=4 Green k=1.5 Light Blue As k is varied, the shape of the graph changes. When k=1 the graph is a circular shape with one curve in the middle. When k=2, the graph has two large and two small "petal" shape. The same is true when k=3, it has 3 large and three small "petal" shapes. When k=4, it has 4 large and 4 small "petals". When k=1.5, the graph has two large "petals" and one small petal. All of these graphs have the same shape as the earlier equation of sin( ), that is in the same form as this equation. The difference is the graphs have been shifted again to center around the x-axis instead of the y-axis for the sin( ) equations.
In the last graph, b is set equal to 1,2,3,1.5,0 and a and k are set equal to 1. Key: k=1 Purple k=2 Red k=3 Blue k=1.5 Green k=0 Light Blue As b is varied, the graph also changes shape and size. In this graph, it is exactly like the earlier graph of the sin( ) equation in the same form. Again this graph is centered around the x-axis instead of the y-axis with the sin equation.
Part 5 Graph of the polar equation given below with c, a, b, and k varied. In the first graph, c is set equal to 1,2,3,4, and -1, and a, b, and k is set equal to 1. Key: c=1 Purple c=2 Red c=3 Blue c=4 Green c=-1 Light Blue In this set of graphs, we have a linear function. As c changes from 1 to 4 the graph is moved to the right on the x-axis, and when c=-1, it is on the left side of the x-axis. Each line crosses the x-axis at c, and each line is parallel. Therefore each line has the same slope. Therefore, we can see from these graphs that this function is linear when a, b, and k is equal to 1. We have also seen from this graph that c effects the shifting of the graphs to the right or the left on the x-axis.
In the second set of graphs, a is set equal to 1,2,3,-1, and 0 and c, b, and k is set equal to 1. Key: a=1 Purple a=2 Red a=3 Blue a=-1 Green a=0 Light Blue As in the previous set of graphs, this graph consists of linear functions. As a is varied, the graphs slope is changed, but each graph has the same y-intercept at (0,1). When a=0, we have a horizontal line. This would be an example of a "pencil" of lines where each line has a different slope but they all intersect at one point. Therefore, we can see from this graph that a effects the slope of the graph but does not effect the shifting of the graph on the coordinate system.
In the third graph, b is set equal to 1,2,3,-1,0 and c, a, and k are set equal to 1. In this set of graphs, where b is varied, the graphs are also linear. They all have different slopes and have the same x-intercept at (1,0). When b=0, the graph is a vertical line. This would also be an example of a "pencil" of lines. Therefore, we can see from this graph that b does effect the slope of the line and not the shifting of the line on the coordinate system.
In the last graph, k is varied from 1 to 4 and a, b, and c is set at 1. Key: k=1 Purple k=2 Red k=3 Blue k=4 Green In this set of graphs, k does effect the shape of the graph. In the first graph, k=1 is a linear function. When k=2, the graph changes to two parallel lines intersecting two other parallel lines. When k=3, we have three lines where all three intersect. When k=4, we have three sets of parallel lines intersecting. Therefore, we can surmise from this graph that when k is even we will have parallel lines intersecting and when k is odd we will have non parallel lines intersecting each other.
Conclusion In all of these graphs, we have seen that k does effect the shape of the graph in each one. In most of the graphs a effects the size, and it never effects the shape. B in most of the graphs slightly effects the shape and does effect the size. In the last set of graphs c only effected the shifting of the lines. We have also seen that there is a great similarity between the cos and sin graphs in each of these problems.