In this assignment, we were to use a spreadsheet to do an exploration of some topic in mathematics.  I choose to do problem 4, which was to generate a Fibonnaci sequence using a spreadsheet.  First, lets discuss what the Fibonnaci sequence is and how to generate it.

    Fibonacci sequence is a sequence of numbers where you start off with two numbers called f(0) and f(1).  To find the next number in the sequence, you add f(0) and f(1).  To find the fourth number in the sequence, you add the third number to f(1), and so on.  So each number after the first two numbers, is the sum of the two previous numbers.  One example is given below.

If f(0)=1 and f(1)=2, then the sequence would be 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, etc....

Using variables to show the sequence, we can say that f(n) = f(n-1) + f(n-2).

   In this assignment, we will look at several examples of the Fibonacci sequence, and we will explore the ratios of the adjacent terms in the Fibonnaci sequence.

     In our first example, lets say that f(0)=0 and f(1)=1.  We are going to use Microsoft Excel to explore the sequence and the ratios of adjacent terms.  Here is the result.

0	0	0	0	0
1	1	0.5	0.33333333	0.2
1	0.5	0.33333333	0.2	0.125
2	0.66666667	0.4	0.25	0.15384615
3	0.6	0.375	0.23076923	0.14285714
5	0.625	0.38461538	0.23809524	0.14705882
8	0.61538462	0.38095238	0.23529412	0.14545455
13	0.61904762	0.38235294	0.23636364	0.14606742
21	0.61764706	0.38181818	0.23595506	0.14583333
34	0.61818182	0.38202247	0.23611111	0.14592275
55	0.61797753	0.38194444	0.2360515	0.14588859
89	0.61805556	0.38197425	0.23607427	0.14590164
144	0.61802575	0.38196286	0.23606557	0.14589666
233	0.61803714	0.38196721	0.2360689	0.14589856
377	0.61803279	0.38196555	0.23606763	0.14589783
610	0.61803445	0.38196619	0.23606811	0.14589811
987	0.61803381	0.38196594	0.23606793	0.145898
1597	0.61803406	0.38196604	0.236068	0.14589804
2584	0.61803396	0.381966	0.23606797	0.14589803
4181	0.618034	0.38196601	0.23606798	0.14589804
6765	0.61803399	0.38196601	0.23606798	0.14589803
10946	0.61803399	0.38196601	0.23606798	0.14589803
17711	0.61803399	0.38196601	0.23606798	0.14589803
28657	0.61803399	0.38196601	0.23606798	0.14589803
46368	0.61803399	0.38196601	0.23606798	0.14589803
75025	0.61803399	0.38196601	0.23606798	0.14589803

   In the first column, we have the Fibonnaci sequence.  In the second column of numbers, we have the ratio of each pair of adjacent terms.  In the third column, we have the ratio of every second term.  In the fourth column we have the ratio of every third term.  In the fifth column we have the ratio of every fourth term. 

   In the first column, we can see that as f(n) increases its value increases.  The numbers get larger very quickly.  From f(0) to f(25), we have gone from 0 to 75,025.  Therefore, we can see that in the Fibonnacci sequence we have a very rapid rate of increase in the numbers. 

   In the second column, we have the ratio of the adjacent numbers in the sequence. For example, the first number is the ratio of f(0)/f(1) or 0/1 which is equal to zero.  The second number is the ratio f(1)/f(2) or 1/1 which is equal to 1, and so on.  We can see that the ratio of adjacent numbers has the limit of 0.61803399.  This number is approximately the Golden Ratio which is seen below.

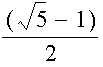
    In the third column, we have the ratio of every second term in the sequence.  For example, the first term is f(0)/f(2) or 0/1 which equals 0.  The second term is f(1)/f(3) or 1/2 which equals 0.5, and so on.  This set of ratios also has a limit.  The limit here is 0.31896601.

    In the fourth column, we have the ratio of every third term in the sequence.  For example, the first term is f(0)/f(3) or 0/2 which equals 0.  The second term is f(1)/f(4) or 1/3 which equals 0.33333..., and so on.  This set of ratios has the limit 0.23606798. 

    In the fifth column, we have the ratio of every fourth term in the sequence.  For example, the first term is f(0)/f(4) or 0/3 which equals 0.  The second term is f(1)/f(5) or 1/5 which equals 0.2.  This set of ratios has the limit 0.14589803. 

In our second example lets use a special Fibonnaci sequence called the Lucas sequence where f(0)=1 and f(1)=3.  Lets also look at the ratios of adjacent terms and their limits as well.  Here is the result.

1	0.33333333	0.25	0.14285714	0.09090909
3	0.75	0.42857143	0.27272727	0.16666667
4	0.57142857	0.36363636	0.22222222	0.13793103
7	0.63636364	0.38888889	0.24137931	0.14893617
11	0.61111111	0.37931034	0.23404255	0.14473684
18	0.62068966	0.38297872	0.23684211	0.14634146
29	0.61702128	0.38157895	0.23577236	0.14572864
47	0.61842105	0.38211382	0.2361809	0.14596273
76	0.61788618	0.38190955	0.23602484	0.14587332
123	0.61809045	0.38198758	0.23608445	0.14590747
199	0.61801242	0.38195777	0.23606168	0.14589443
322	0.61804223	0.38196916	0.23607038	0.14589941
521	0.61803084	0.38196481	0.23606706	0.14589751
843	0.61803519	0.38196647	0.23606833	0.14589823
1364	0.61803353	0.38196584	0.23606784	0.14589796
2207	0.61803416	0.38196608	0.23606803	0.14589806
3571	0.61803392	0.38196599	0.23606796	0.14589802
5778	0.61803401	0.38196602	0.23606798	0.14589804
9349	0.61803398	0.38196601	0.23606797	0.14589803
15127	0.61803399	0.38196601	0.23606798	0.14589803

        In our first column, we have the Fibonnaci sequence of numbers.  As you can see in this example, the set of numbers also rapidly increase.  Next lets look at the ratios of the adjacent terms.  In the second column, we have the ratio of each pair of adjacent terms.  We can see that the limit is the same in this example as in the first one, 0.61803399.  In the third column, we have the ratio of every second term.  In this set of ratios we also have the same limit as before, 0.38196601.  In the fourth column, we have the ratio of every third term.  We also have the same limit as before, 0.23606798.  In the fifth column, we have the ratio of every fourth term.  We also have the same limit as before, 0.14589803.

    In the next example, lets use f(0)=1 and f(1)=4 and see what happens to the sequence and the ratio of terms.

1	0.25	0.2	0.11111111	0.07142857
4	0.8	0.44444444	0.28571429	0.17391304
5	0.55555556	0.35714286	0.2173913	0.13513514
9	0.64285714	0.39130435	0.24324324	0.15
14	0.60869565	0.37837838	0.23333333	0.1443299
23	0.62162162	0.38333333	0.2371134	0.14649682
37	0.61666667	0.3814433	0.23566879	0.14566929
60	0.6185567	0.38216561	0.23622047	0.1459854
97	0.61783439	0.38188976	0.23600973	0.14586466
157	0.61811024	0.38199513	0.23609023	0.14591078
254	0.61800487	0.38195489	0.23605948	0.14589316
411	0.61804511	0.38197026	0.23607122	0.14589989
665	0.61802974	0.38196439	0.23606674	0.14589732
1076	0.61803561	0.38196663	0.23606845	0.14589831
1741	0.61803337	0.38196577	0.2360678	0.14589793
2817	0.61803423	0.3819661	0.23606805	0.14589807
4558	0.6180339	0.38196598	0.23606795	0.14589802
7375	0.61803402	0.38196602	0.23606799	0.14589804
11933	0.61803398	0.38196601	0.23606797	0.14589803
19308	0.61803399	0.38196601	0.23606798	0.14589803

   In the first column, we can see the sequence of numbers increases rapidly again.  We can also see that the limits of the ratios of the next four columns are the same as they were in the first two examples.  Therefore, we can make the conjecture that the limits of the ratios will always be the same for any Fibonnaci sequence.  The limit of the ratio of every pair of adjacent term will always be 0.61803399.  The limit of every second term will always be 0.38196601.  The limit of every third term will always be 0.23606798.  The limit of every fourth term will always be 0.14589803. 

   We could look at many other examples of the Fibonacci sequence for different f(0) and f(1) and get the same results. 

Return.