
EMAT 6680
Assignment 7: Tangent Circles
Problem #4
By
Laura King

EMAT 6680
Assignment 7: Tangent Circles
Problem #4
By
Laura King
In this assignment, we were supposed to investigate tangent circles to two given circles. We were also supposed to investigate the locus of the centers of the tangent circles. I choose to do problem #4. In problem #4, we are going to discuss the locus of centers for different cases of circles.
Part 1
In the first set of examples, we will look at problems where one of the given circles is inside the other circle. We will look at examples where the designated point for the tangent circle is on both the larger circle and the smaller circle.
Point on the larger circle
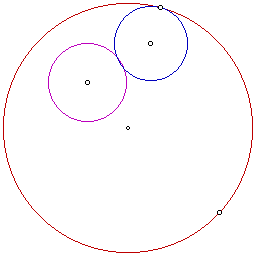
The tangent circle here is the blue circle. It is tangent to both the red and the purple circle. Next we will look at the locus of circles for the tangent circle as the designated point is moved around the red circle.
Click here if you would like to use a gsp script to draw a circle tangent to two other circles. You will need to create the required four points to do the construction.
Locus of centers for tangent circle
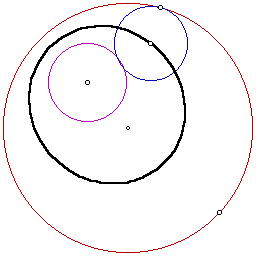
In this example, the locus is an ellipse. The foci of the ellipse are the centers of the two given circles. Next we will look at the construction of the tangent circle when the designated point is on the smaller circle.
Click here if you would like to see the animation of the construction of the locus.
Point on the smaller circle
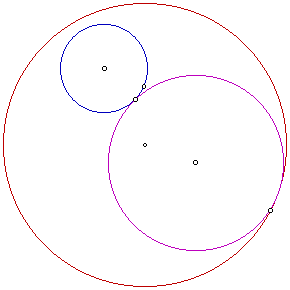
The tangent circle in this drawing is the purple one. The designated point here is on the smaller circle, which is blue. Next we will look at the locus of the centers for the tangent circle as the designated point moves around the blue circle.
Locus of centers for tangent circle
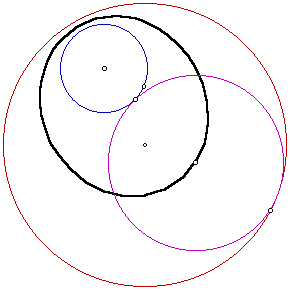
As in the previous example, the locus of centers is an ellipse. Also like the previous example, the foci for the ellipse is the centers of the two given circles. Next we will look at an example where the smaller circle is internal to the tangent circle.
Smaller circle internal to the tangent circle
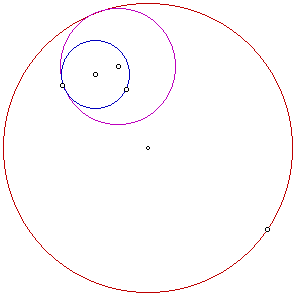
The tangent circle is the purple circle in this example. It is inside the smaller circle and is tangent to both circles. Let's look at the locus of centers for the tangent circle as the designated point moves around the blue circle.
Locus of centers for the tangent circle
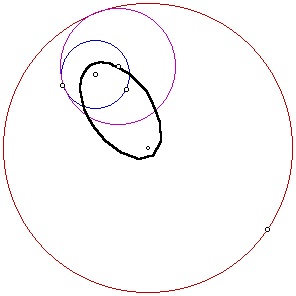
As in the previous two examples, the locus of centers for the tangent circle is an ellipse. The foci are still the centers of the two given examples.
We could look at many more examples where one circle is inside of the other circle and the result will still be the same. Therefore, we can make the conjecture that when one circle is inside of the other circle the locus of the centers of the tangent circle will always be an ellipse. Also, we can make the conjecture that the foci of the ellipse will always be the centers of the two given circles.
Part 2
In the second part of the problem, we will look at the tangent circles to two circles that intersect. We will also look at the locus of centers of the tangent circles.
Tangent circle to two circles that intersect
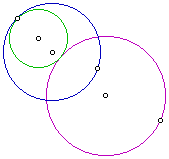
The tangent circle in this example is the green circle. It is inside of the smaller circle which has the designated point on it. Next lets look at the locus of centers of the tangent circle as the designated point is moved around the circle.
Locus of centers of the tangent circle
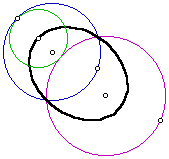
Again in this example, the locus is an ellipse with its foci being the centers of the two given circles. Next lets look at an example where the designated point is on the larger circle.
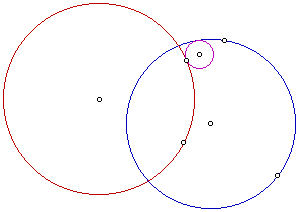
Our tangent circle is the purple circle in this example. The designated point in this sketch is on the larger circle, which is red. Next let's look at the locus of centers for the tangent circle as the designated point traces the red circle.
Locus of the centers of the tangent circle
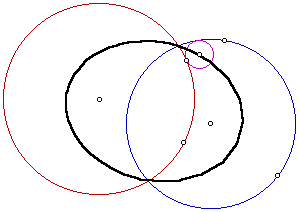
As in all of the previous examples, we again have an ellipse as our locus with the foci of the ellipse the centers of the two given circles. Therefore, we have seen that when the two circles intersect the locus of the centers is still an ellipse with the foci of the ellipse the centers of the two given circles.
Part 3
In this part of the problem, let's look at examples where the two given circles are tangent to each other. We will also look at the locus of the centers of the tangent circles.
Tangent circle to two tangent circles
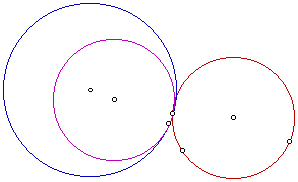
In this drawing, the tangent circle is blue. Let's look at the locus of the centers of the tangent circle.
Locus of centers of the tangent circle

The locus in this example is not an ellipse. It is a kind of linear path that ends. So we have seen here that when the two given circles are tangent, the locus of centers is affected. Let's look at another example of this where the two given circles are tangent.
Tangent circle to two tangent circles

Our tangent circle again here is blue. Lets see what the locus of the centers of this tangent circle looks like.
Locus of centers of the tangent circle
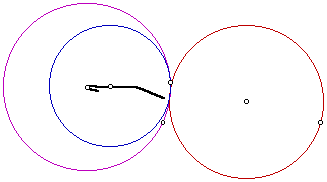
Here our locus is still not an ellipse. It is not linear in this example either. It is a kind of crooked line that seems to curve at one end. Therefore, we have seen here that when the two given circles are tangent the locus of centers is greatly changed. It is not the same in each example, but it definitely does not make an ellipse.
Part 4
In the last set of problems, we will look at examples where the two given circles are disjoint. We will look at the locus of centers of the tangent circle for each example.
Tangent circle to two disjoint circles
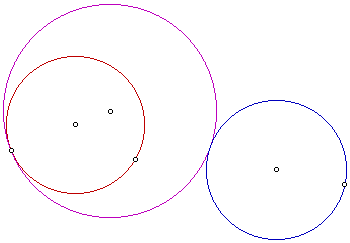
In this sketch, the tangent circle is purple. The designated point is on the red circle. Next let's look at the locus of centers for the tangent circle.
Click here to see a drawing of the locus of the centers of the tangent circle.
Locus of centers of tangent circle
If you look at the sketch, you will see that the locus of centers is not al elliptical shape in this example. It is a hyperbolic shape where the foci of the hyperbola are the centers of the two given circles. Next lets look at another example of two disjoint circles and their tangent circle.
Tangent circle to two disjoint circles
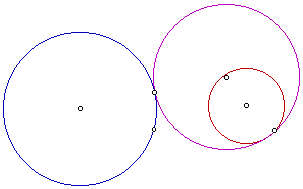
In this example, the tangent circle is purple. The designated point in this problem is on the blue circle. Let's look at the locus of centers of the tangent circle.
Click here to see a drawing of the locus of centers of the tangent circle.
If you look at the drawing, you will see again that the locus of centers of the tangent circle forms a hyperbolic shape where the two foci of the hyperbola are the centers of the two given circles. Therefore, we have seen from these sketches that when the two given circles are disjoint the locus of the centers of the tangent circles form a hyperbolic curve with the foci the two centers of the given circles.
Conclusion
In the first two parts of this assignment we looked at examples where the two circles intersected or one circle was inside of the other. In each of these cases, the locus of the centers of the tangent circles was an ellipse. In the all of the ellipses, the foci was the centers of the two given circles. In the third part of the assignment, we looked at the case where the two given circles were tangent to each other. In this case, the locus of the centers of the tangent circles did not have a definite shape. It is not an ellipse nor is it a hyperbola, like in part four. Therefore, we cannot give an exact shape for this case. In the last part, we looked at circles that were disjoint. In each of these sketches, our locus of centers of the tangent circle has a hyperbolic shape. In each hyperbola, the foci are the centers of the two given circles. Also, in each of the drawings on of the given circles is inside of the tangent circle. Therefore, we can make the conjecture that this will hold true for any of these four cases.