
EMAT 6680
Assignment 8: Altitudes and Orthocenters
Problem # 1-8
By
Laura King

EMAT 6680
Assignment 8: Altitudes and Orthocenters
Problem # 1-8
By
Laura King
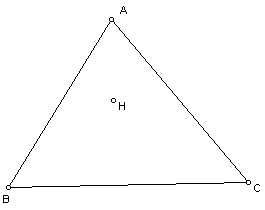
In this assignment, we will explore the orthocenter of a triangle and the three triangles formed by the segments joining the orthocenter and each vertex of the triangle. The orthocenter of a triangle is the common intersection of the three lines containing the altitudes.
In our first drawing, we have the orthocenter of our original triangle ABC.
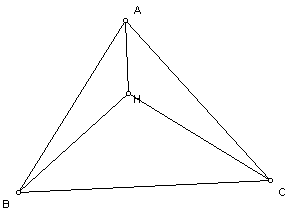
Next we will look at the three triangles formed by connecting the orthocenter of the triangle to each of the vertices.
Next we will look at the orthocenter of each of the three triangles formed HBC, HAB, and HAC. Notice that each of the triangles formed is an obtuse triangle, which means that one of the angles in each triangle is greater than 90 degrees. Whenever we get the orthocenter of an obtuse triangle, the orthocenter is outside the triangle. Our original triangle was an acute triangle and that is why the orthocenter was inside of the triangle.
Orthocenter of triangle HBC
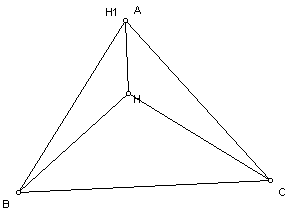
Orthocenter of triangle HAB
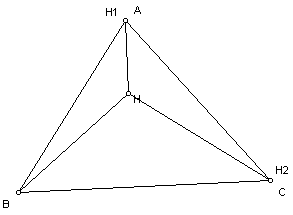
Orthocenter of triangle HAC
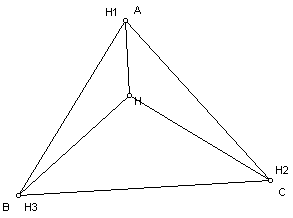
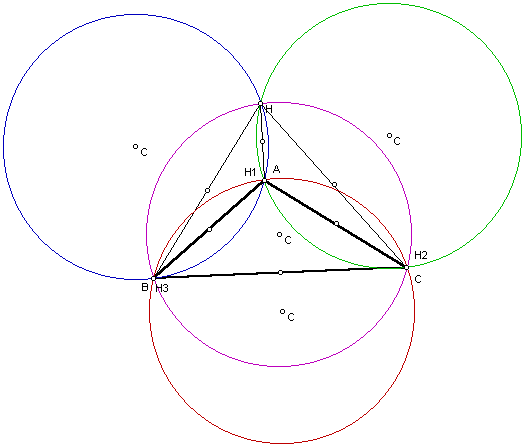
Notice that the orthocenter of triangle HBC, H1, is at the third vertex of the original triangle, A. Also the orthocenter of triangle HAB, H2, is at the third vertex of the original triangle, C, and the orthocenter of triangle HAC, H3, is at the third vertex B. Therefore, we can make the conjecture that in each of the triangles formed by connecting the orthocenter of a triangle to each of the vertices the orthocenters will be the third vertex of the original triangle.
Next we will look at the circumcircles of the original triangle and each of the three triangles formed by connecting the orthocenter to each vertex of the original triangle.
Circumcircle of triangle ABC
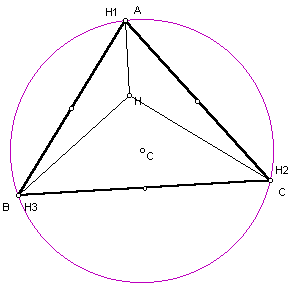
Circumcircle of triangle HBC
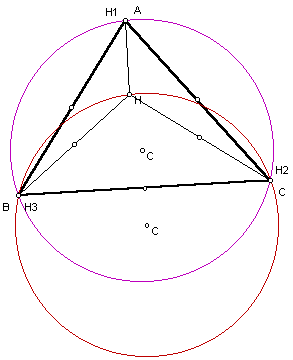
Orthocenter of triangle HAB

Orthocenter of triangle HAC
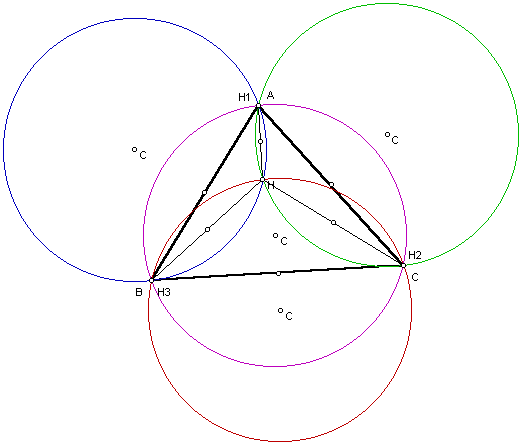
Notice that each of the four circles looks to be the same size. Click here to see a gsp sketch where the radius of each circle has been measured. They are the same size for this drawing. You can also change the size of the triangle by moving the vertex and the circles will still remain the same size as each other.
Next we will look at what happens when you move the vertex of the original triangle ABC to its orthocenter H. You can click here to see a gsp sketch with movement keys to move each vertex to H. Below is one example where A is moved to H.
Movement of vertex to orthocenter
You can see from the drawing that H moves to where A originally was in the drawing. When each of the vertices is moved to where H is, the same thing happens. The new triangle ABC is an obtuse triangle for each movement. We know from the previous example that in an obtuse triangle the orthocenter is always outside the triangle. That is why the H moves outside triangle ABC in each translation of the vertex. You can try this with different triangles by moving the vertices ABC around and the results will still be the same.
Therefore, we can make the conjecture that whenever the original vertex of a triangle is translated to its orthocenter, H, H will be translated to the vertices original position. Also, we can say that the new triangle formed will be an obtuse triangle.
The last drawing we will look at here is the drawing of the nine point circle for the original triangle ABC.
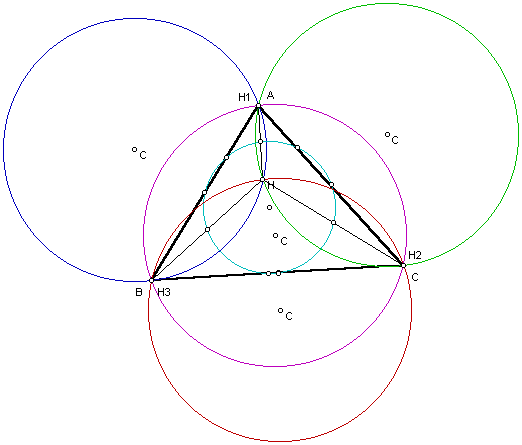
If you try to construct the nine point circle for
the other three triangles HBC, HAC, and HAB, the nine point circle will
remain the same. Therefore, we can make the conjecture that for the
three triangles formed by the segments connecting the orthocenter ,H, of
a triangle and its three vertices will all have the same nine point circle
as the original triangle.