

We want to use our graphing calculator program on this assignment to see what happens to the graph of our equation for n values ranging from 2 to 25. Let's begin our investigation for the case n=2:
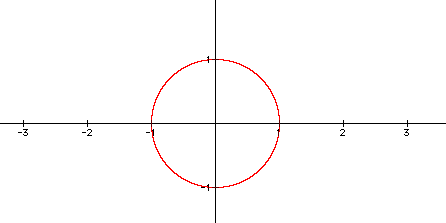
We notice that for n=2 we get a circle, with center at the origin and radius of 1. This is what I expected, because we know our equation is the standard form equation of a circle. Now let's look at the case for n=3. I am assuming that this equation will not produce another circle based on what I know about cubes:
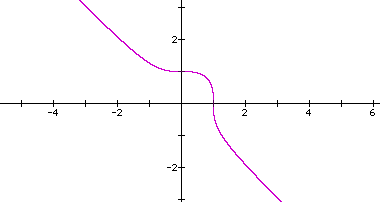
We can see that our graph is not that of a circle, as our first graph was. It appears to be a descending graph across the line y=-x. As it approaches zero we notice our graph curves around the path of our circle for n=2. An interesting thing to see would be both graphs on the same axes:
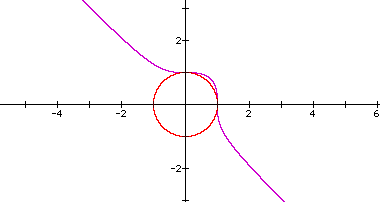
We can clearly see the path of the graph for n=3 (in purple) as it curves around the circle, which was for n=2 . Let's investigate further using n=4 and n=5
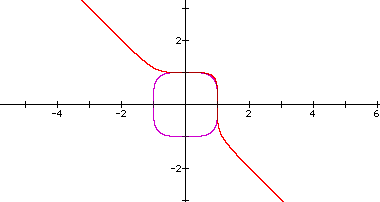
The graph for n=4 is in purple and the graph for n=5 is in red. We noticed that for n=2 we produced a circle and for n=3 we produced a graph that "traced" around or is tangent to the cicle. For n=4 we notice our graph is similar to the case of n=2, except the graph has become more angular, less circular. We also notice that for n=5 we generated a graph that "traces around" or is tangent to the graph of the previous case. Let's see if that pattern holds for n=6 and n=7:
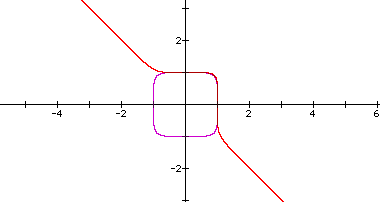
We can clearly see the pattern continuing for n=6 (purple) and n=7 (red). First, we notice that the graph for n=6 is "similar" to the cases of n=2 and n=4 in that they are all enclosed graphs. However, the graph of the case for n=6 is more angular than for n=4, just as n=4 was more angular than n=2. In fact, it appears that the graphs for n=even # will all be enclosed. Furthermore, it appears that the graphs for n=odd # will "trace" around the graph of the equation for n= odd #-1. Now, let's look at the cases for n=24 and n=25:
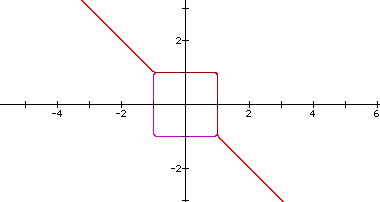
The graphs for the cases of n=24 (purple) and n=25 (red) give a clear picture to what is happening as n increases. We notice that the case of n=24 gives us a graph that is almost a perfect square. Recalling that the case of n=2 yielded a perfect circle, we can see that for n= even # we get graphs that are increasingly more angular in shape, to the point that we have a square. We also notice that the case for n=25 holds to the pattern of the previous cases for n= odd # by "tracing" around the case for n=24. If we investigated further I am confident that we will see a continuation of these patterns we have discussed.