

This assignment deals with the nature of quadratics, given a standard form equation. Basically we are working with equations of the form:
In this particular problem, we begin with the quadratic equation:
This is a quadratic equation in standard form, where a=2, b=3, and c=-4. Before we do any further investigations with this equation, let's see how the graph will look:
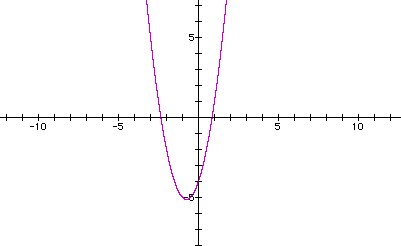
Now, let's see what hapens when we replace all of our x values with (x - 4):
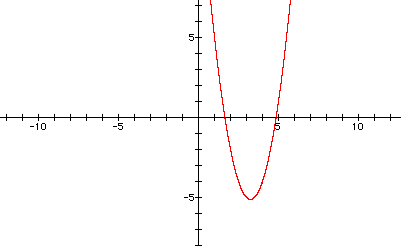
As we can see, the graph has shifted to the right by 4, but that was to be expected.
Question: How can we get our graph to move to the second quadrant?
Well, we moved our graph to the first quadrant by replacing x with (x - 4). Therfore, it stands to reason that we could move the graph to the second quadrant simply by replacing x with (x + 4). Let's see how that paticular graph will look:
A nice thing to see would be all three graphs on the same axes:
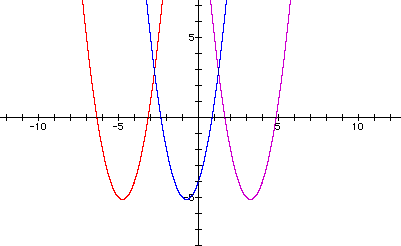
Here, we can clearly see what happens when we replace x {in blue} with (x - 4) {in purple}, and then wth (x + 4) {in red}. We get graphs that have been shifted horizontally.
Question: How can we produce a graph which is concave down that shares the same vertex as our original?
Well, the first thing we need to do is rewrite our equation in vertex form. Then simply add a negative to the front of the equation. This yields:
Let's see how the two graphs look on the same axes:
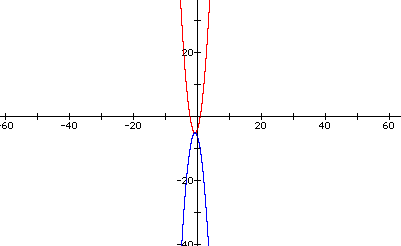
We have seen in this investigation how we can manipulate a quadratic equation to get a particular "desired" result. I'm sure there are several other things we could have manipulated, these were just a few.