

This assignment was one in which our goal was to investigate tangent circles. I worked with this process for a while. One interesting construction I created was finding the two tangent circles to two original circles, one inside the other. One tangent circle is external to the smaller circle (Click Here) and the other is internal to the smaller circle ( Cltck Here) . Let's see how this will look:
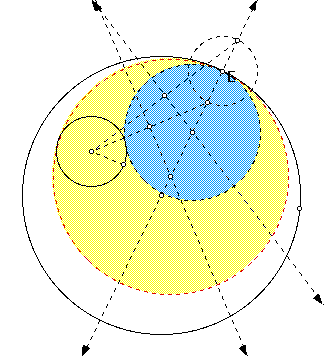
For a script of this GSP sketch Click Here. Notice that both tangent circles (shaded yellow and blue) are tangent to the same given point on the original large circle
Hopefully, now we can see that the locus of the centers ,as E rotates around, of the circles is the shape of an ellipse (red).
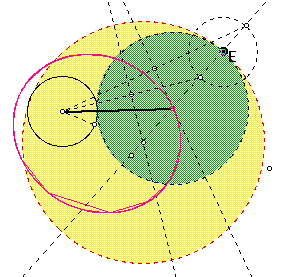
Now let's assume that the original circles intersect. Let's see how the tangent circles would look:
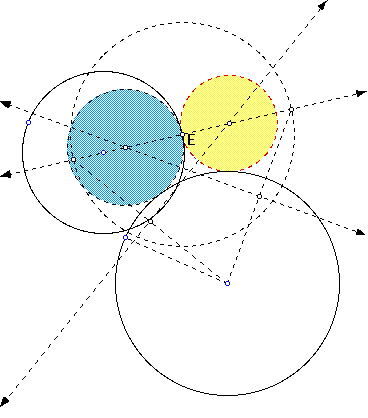
Now, let's look at the locus of points of the centers of the tangent circles:
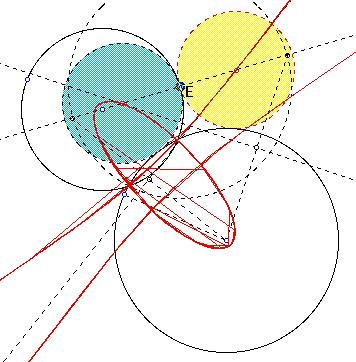
I'm not quite sure how to explain what I'm looking at. It appears that the shape traced by the locus of points of the centers of the tangent circles gives an ellipse, together with a hyperbola.
Next, let's take the case of disjointed triangles and see where the tangent circles lie, as well as the locus of points of the centers of the tangent circles. Let's see how it will look:
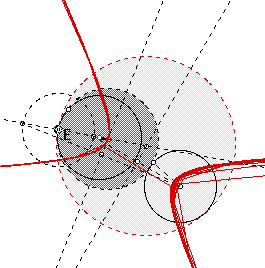
Notice, that the locus of points of the centers form a what appears to be a hyperbola(in red).
When I considered the locus of the midpoint of the segment that formed the base of the key isosceles triangle of each set of circles, there was nothing that I would consider out of the ordinary. The traced paths look similar to the paths of the locus of points of the centers.