

In this assignment we will examine pedal triangles. Given any triangle ABC, if point P is any arbitrary point in the plane, then the triangle formed by constructing the perpendiculars and connecting their intersections with the sides of ABC yields a pedal triangle, for my pedal point P.
Now, I want to construct a pedal triangle. Given triangle ABC, I want to find pedal triangle RST, where R , S, and T are the intersections of the perpendiculars and the sides of ABC. Let's see how this will look:
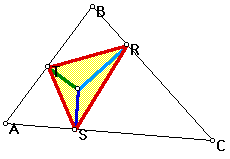
To see a script of this Click Here.
Question?: What if point P is the centroid of triangle ABC?
Well, to get a good understanding of this idea Let's construct our centroid first, then run our script of the pedal triangle. Let's see how this will look:
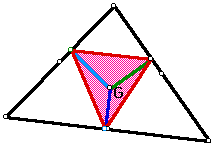
I think a more interesting problem is the next question.
Question?: What if P is the incenter?
Well, let's construct this scenario and find out:
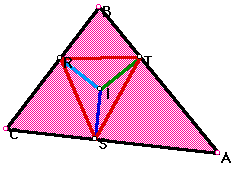
This is a very interesting case. After I constructed the pedal triangle where point P is the incenter I noticed that the lengths of the segments RI, TI, and SI looked similar. This caught my eye so measured the lenthgs of each. In fact, all three lengths were the same. Furthermore, these three segments represent the minimum distance to each side. We know this because these segments form right angles with the sides of the original triangle ABC.
Now, let's look at the segments CT, BS, and AR. A picture would be nice:
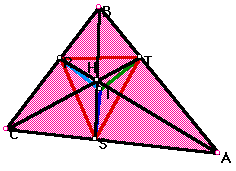
From this we can see that segments CT, BS, and AR are concurrent at point H.
Now, I want to look at the relationship between the pedal triangle and the incircle. First let's get a look of this:
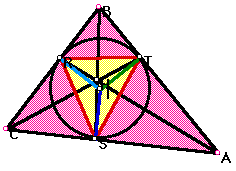
Looking at this, we can clearly see a relationship between our pedal triangle and the incircle. It appears that the incircle goes through the vertices of the pedal triangle with pedal point I. This is a very interesting result. We could have probably figured this out intuitively, because of the knowledge that the lengths between incenter and the three vertices are all equal.