

Mathematics can be found in most every workplace environment. In many cases, it is easy see exactly where the math would be used. I was in the process of looking for a workplace that, in fact, used mathematics when I stumbled upon an area that one would never have thought of. I was talking with my father, who has been an angus cattle farmer for around 30 years, when I realized that math can be used even in his field. In fact, it was presented to me in a problem that he proposed. This was an excellent problem to show there is little difference between conventional math and the "mathematics" of a farmer.
Obviously, during the winter months there is no grass in the fields for the cattle. So, to have sufficient feed for them my father uses a particular pasture in which he bales hay to store for the winter. From experience, he knows that he needs 1,000 bales to make it through the cold spell. He must keep the herd out of this field during the warm months so the grass will have plenty of time to grow to acceptable cutting length. This seems as if the plan is simple and easy to follow. However, there are several factors that play a part in this particular endeavor. First of all, my father has only enough money for one cutting per year. However, he cannot let the grass in the field grow too large, because the gentleman that bales the hay charges per bale. Keeping this in mind, my father wants to have a cutting as close to 1,000 bales as possible to, on one hand, have enough feed for the winter, yet to also keep the cost to a minimum. For a person with no experience in this process, this might seem like a daunting task. However, for my father, this is not hard at all. By knowing the size of his field and having years of experience, he knows almost exactly how high to let the grass grow to reach his quota, while keeping costs down at the same time. He told me, for a perfect size cutting, the grass needs to be approximately one and a half feet (18 inches) high. He then asked me, having no experience, how would I figure out approximately how high to let the grass in the hay field grow to assure myself of having around 1,000 bales.
Thinking along mathematical lines, there were a couple of questions to which I needed answers.
Question-1: What are the general shape and dimensions of the field?
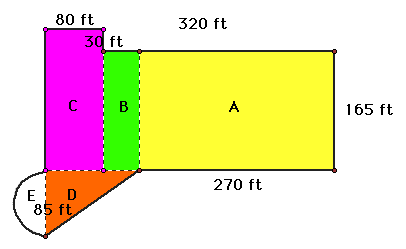
Question-2: Approximately how much grass makes one bale of hay?
Remember, using farmer's knowledge, my father estimated that to get roughly 1,000 bales the grass needs to be approximately one and a half feet high. We will now use conventional mathematics to prove, or disprove, the accuracy of "farmer's mathematics".
The first step I would take is to find the total area of the pasture. Looking at the diagram above, I see that I have three separate shapes within the field: a rectangle, a triangle, and a semicircle. In order to find the total area, I need to find the areas of each of the five individually divided sections ( A, B, C, D, and E), then take the sum of those areas. I will need to use the following formulas in my calculations:
Calculations:
Area (A) = 270 x 165 = 44,550
Area (B) = 165 x 150 = 8,250
Area (C) = 80 x 30 = 2,400
Area (D) = 1/2 x 85 x 110 = 4,675
Note: the area for the semicircle can be approximated by the area for a sector of a circle. In our case, since the diameter of the semicircle is 85 ft, we know the radius = 1/2 diameter = 42.5 ft
![]()
Now that we have found the areas for each individual section, we can take their sum to find the total area:
Area (total) = A + B + C + D + E = 44,550 + 8,250 + 2,400 + 4,675 + 2,837.25
Recall, that given grass height = 1 foot, we need approximately a 10 x 10 area of grass to make one bale. Now, let's see how many 10 x 10 areas we have in our field of area 62,712.25 square feet. Well, 10 x 10 = 100, so:
Now, if the grass is one foot high, then we can say that we will get approximately 627 bales. Obviously, this falls well shy of our goal of 1,000 bales. In fact, we fall about 373 bales shy, or approximately 373/627 = .59489 = 59.5% more bales.
Well, 59.5% of one foot is about 7.14 inches, implying that is the height we need to add to our current height of one foot.
Thus, to get approximately 1,000 bales in the given field we need a grass height of about one foot and 7.14 inches . Of course, given the error that may occur, this estimate might be as much as an inch off. Amazingly, this put's the grass height right at the height my father suggested he would need, about one and a half feet. I guess this proves that the math of a farmer is just as reliable, in his field of expertise, as conventional mathematics.