

Problem: Consideer any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.
First, let's get a look at the sketch of this problem:
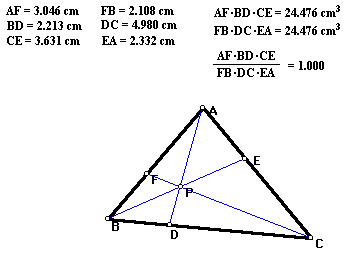
Well, from looking at this problem via GSP there are a couple of things that can be concluded. First of all, we can see that (AF)(BD)(CE) = (FB)(DC)(EA) for all triangles and for all points P. By this, we know that the ratio (AF)(BD)(CE) / (FB)(DC)(EA) always equals 1. I looked at multiple triangles, along with multiple points P, and found this to be true. To go to a working GSP sketch of this Click Here.
We want to prove that this indeed is true, so let's begn by using the hint (i.e., drawing parallel lines to produce similar triangles). Let's explore this using GSP:
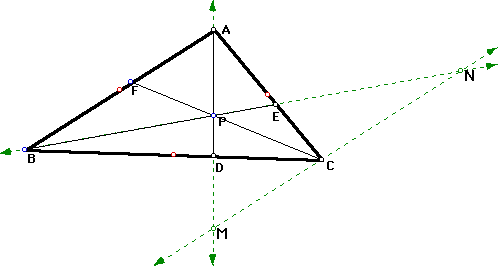
So, I constructed line MN to be parallel with line AB. This, indeed, gives us a few similar triangles: CPM and APF, CPN and BPF, CEN and AEB, CDM and BDA. From this we can begin to set up some ratio equalities.
Now that we have these ratios, we can use them to substitute in:
Well, that is what we were hoping to prove. Let's move on.
Question?: Can the result be generalized (using lines rather than segments to construct ABC) so that point P can be outside the triangle?
Well, by looking at a GSP sketch, and manipulating it, we can clearly see that P can be outside the triangle. To view a working GSP sketch of this Click Here. Play with this by moving around the vertex A.
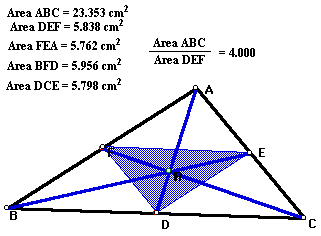
Problem: Show that when P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. When is it equal to 4?
Let's look at a working GSP sketch to illustrate the first part of this problem. To see this Click Here. Manipulate the graph by moving around point P. You can clearly see that the ratio of the areas of triangles ABC and DEF will always be at least 4.
So when will the ratio be exactly 4? The first thing I thought of would be when point P is actually the centroid.
I constructed this with a GSP sketch and, indeed, found that when I made the centroid my point P the ratio of the areas was exactly 4. Let's see this:
This concludes my investigation.