

Sometime around the fifth century BC there was a Greek Mathematician / philosopher that dabbled in many subjects, including such topics as music, astronomy, number theory, and oh yeah, geometry. In the time he was "fooling around" with these ideas, at some point, he realized that given a right triangle the square of the hypotenuse is equal to the sum of the squares of the sides containing the right angles. Many say this thought was not original to him, but rather, the Babylonians. However, as time went on, this "theorem" was credited to him. More than likely, this is so because he was the first to prove that it was true. Hence, we have "Pythagoras' Theorem". Since Pythagoras' time there have been numerous others whom have found ways to prove or derive his famous theorem. It is truly amazing how many different thought processes can be involved in deriving this formula. Many of them are very similar, however, some stand out from the others. It has been a pasttime through the centuries to find new and inventive ways of deriving the Pythagorean Theorem. In this essay, I have chosen to investigate those that I think are interesting. Furthermore, I tried to chose those that had differing lines of thought, to give a rough idea of all lines of thought. These derivations can be credited to anyone from third century Chinese mathematicians to American presidents. With many of these investigations I will use GSP capabilities to aid me in constructing the figures that one would need for the particular proofs. This is particularly nice to do for high school students who have GSP access, being a good way to illustrate these concepts to them.
The first that I have chosen is one of many "visual" proofs that are out there. Pythagoras, himself, was thinking along these lines. He did not consider the term "square" as a number times itself, or in our thinking, a (side) * (side). He was actually picturing squares when he said the sum of the parts of two squares equal the parts of the third square. The following visual of this is credited tho the Chinese mathematician Liu Hui from the third century AD:
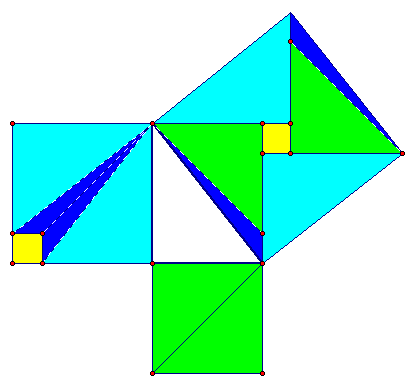
It is clear by this visual that the parts of the square created by one leg of the right triangle and the square created by the other leg of the right triangle can be used to create the third square from the hypotenuse. Like I stated before, there are dozens of visual proofs, but this is the one I found most interesting, and really, the easiest to decipher!
In my opinion, the best proofs are the ones that are the simplest. Here is a proof of Pythagorean's Theorem that anyone could grasp:
Given a right triangle ABC, construct the altitude AD as follows:
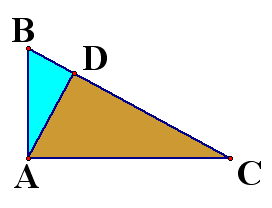
This yields similar triangles ABC, ABD, and ADC, which leads to the following ratios:
From there we can get:
Hence, we have derived the theorem.
There are many other like proofs involving similar triangles and scaling properties, but this one seems to be the most efficient.
Another proof that I like, because it is very distinguishable from the others, is one derived by using Heron's formula. This proof can be credited to William Dunham:
Let sides of a triangle have lengths a,b, and c. Now, let's let the semiperimeter s = (a + b + c) / 2 and let area = A. Then we can introduce Heron's Formula, which states:
For the right triangle with hypotenuse c, we can say that A = (1/2)ab. Also, using the definition of semiperimeter we can note :
Now if we substitute these values into the right-hand side of Heron's Formula we get:
For the rught triangle, this expression is equal to:
we have:
Take all the terms to the left-hand side and regroup to get:
After we factor, we now get:
Finally, factor the preceding perfect square trinomial to get:
To me, this is a wonderful proof, as well as a fabulous use of Heron's Formula. Definitely, there is plenty of algebra in this derivation, but none that an Algebra II student shouldn't be able to handle. This would be great to show a class.
Here is another simple proof I found from Rik's Treehouse website. Again, saying that this proof is simplistic is the highest form of flattery, especially when other proofs of the same theorem are much more complicated. This is a proof that one could show their high school students, while havig no qualms about whether or not they can understand it. The key to this proof, as the writer states, is all in the way you draw it:
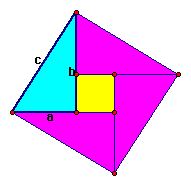
Given a right triangle ( in blue), with legs a,b and hypotenuse c, construct a square with area c squared. Looking at the figure above, we can fit four triangles into the large square, each having area = (1/2) ab, leaving an inner square that has an area = (b -a)(b - a). So, the total area of the bigger square is:
Perhaps, the most interesting proof, not so much for its content, but because of who derived it, is Garfield's Theorem. Fortunately, this is also a really nice proof, sort of an extra incentive to look at it. This proof is so named because it was derived by James Garfield, who just happened to be President of the United States. Let's take a look at it:
Place two right tringles, with sides a,b and hypotenuse c, as such:
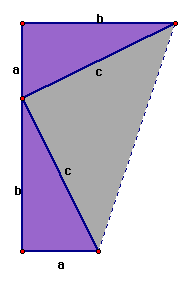
Looking at the figure above, one can clearly see the two congruent triangles (in purple). Also, by connecting the two free vertices of the triangles we construct a trapezoid, having parallel sides of lengths a (base) and b (top), respectively. By constructing the trapezoid, we have created a third triangle, which is isosceles, having equal sides of length c. We will use the fact later on that the Area(trapezoid) = (1/ 2)h(a + b), where a and b are the parallel sides, and h is the height, which in this case is (a + b). So:
After cancelling out the "ab"'s on both sides of the equation we get:
Therefore,
This is a very nice derivation of Pythagorean's theorem. Perhaps, we should call Garfield the "modern Pythagoras" for his efforts. A similar proof is based on the following figure:
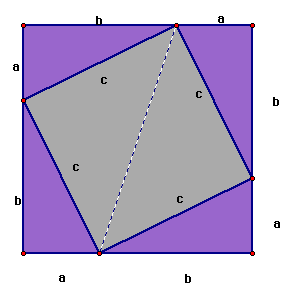
Hopefully, you can clearly see the relationship this and Garfield's theorem.
These were just a few of the derivations of Pythagorean's Theorem that I found enjoyable and interesting. Hopefully, this gives a good variety of the proofs that exist!