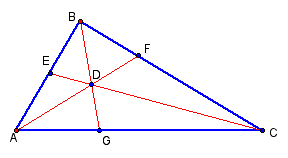
We will begin with a verification of Ceva's Theorem.

Given triangle ABC with cevians BG, AF and CE concurrent at point D, we wish to demonstrate that:
Click here for a GSP 4.0 sketch to investigate.
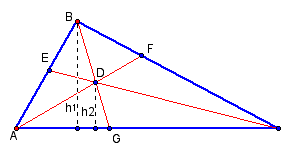
We begin by constructing altitudes h1 and h2. The area of triangle ABG [in the future, we will use the notation (ABG) to designate the area of triangle ABG] equals 0.5(AG)(h1) and (BGC) = 0.5(GC)h1. Also, (ADG) = 0.5(AG)(h2) and (DGC) = 0.5(GC)(h2). Thus,
We conclude, then, that
Similar reasoning yields the equations
Thus,
By cancelation,
We will now consider the converse of Ceva's theorem.

Given,
show that cevians BG, AF and CE are concurrent.
Click here for a GSP 4.0 sketch to manipulate.
Assume that cevians AF and CE intersect at D, and that the other cevian through D is BH. By Ceva's theorem,
Since we assumed
by the transitive property,
Simplifying,
which is true only if H and G represent the same point. Thus, segments AF, CE and BG must be concurrent.
(Reference: Coxeter, H. S. M. & Greitzer, S.
L. (1967). Geometry Revisited. Washington D. C.: The Mathematical
Association of America. 4.)