The following is a graph of the cissoid of Diocles, named in honor of the Greek scholar who was the first to construct the cissoid about 160 B.C.

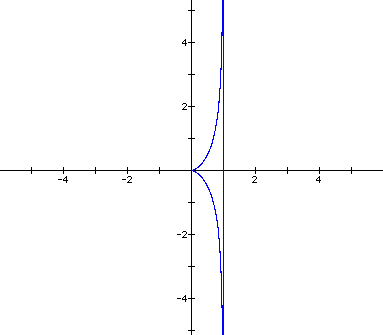
The vertical line x = 1 is an asymptote line for the cissoid. A cissoid can be defined as follows:

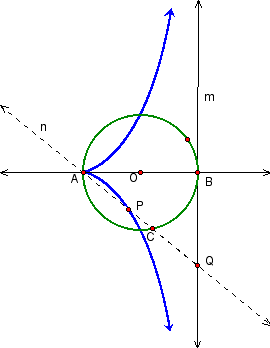
Given circle O with diameter AB. Construct line m perpendicular to secant AB at B. Draw line n through A such that it intersects m. Call the intersection of n and m point Q. Label the intersection of n and circle O as point P. The cissoid is the locus of points P on line n such that AP = CQ (shown in blue in the graph above).

Click here for a GSP 4.0 sketch to manipulate/investigate.

A strophoid is an extension of the cissoid. In the diagram below, we see a construction of a right strophoid.

Line n is perpendicular to ray DO at D. Line m represents all lines through O intersecting line n at Q. The spheroid (shown in blue) is the locus of points P such that QD = QP. Note that the curve to the left of line n is a cissoid.

Click here for a GSP 4.0 sketch to manipulate.

The strophoid below can be represented with the polar equation

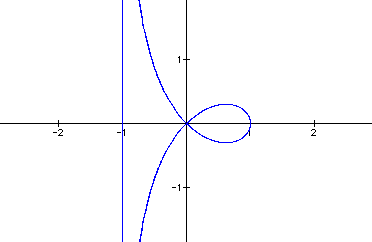
Notice the asymptote line at x = -1.

The strophoids above are right strophoids because lines m and n are perpendicular. What would happen if m and n were not perpendicular? The result is an oblique strophoid. (See an example below.)

(The diagonal blue line and the x-axis correspond to lines n and m of the construction of the right strophoid.)