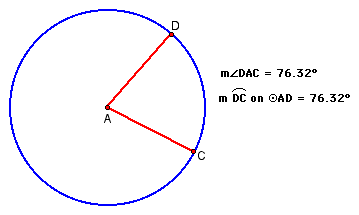
Review: A central angle of a circle is an angle with its vertex at the center of that circle. In the diagram below, angle A is a central angle. The measure of angle A equals the measure of arc CD. (We say that angle A intercepts arc CD.)

Question: In the diagram below, the measure of arc CD equals the measure of arc EF. What is true about angles DAC and EAF? Why?
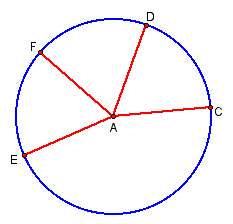
Investigation:
Construct a circle A, then construct four
points on the circle. Label these points C, D, E and F. Construct
chords CD and EF. Construct arcs EF and DC. (To construct arc
EF, click on point E, click on the circle, click on point F and
choose "Arc on Circle" from the Construct menu at the
top of the page. (By the way, we say that chord EF subtends
arc EF.) Measure lengths EF and DC, then measure arc angles EF
and DC. Drag various points until chords EF and DC are congruent.
What appears to be true? Proof? Hint?
Return