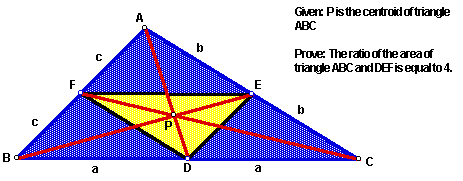
Since P is the centroid of triangle ABC, line segments AD, CF and BE are the medians of triangle ABC and D, E and F are the midpoints of sides BC, AC and AB respectively. Thus, BD = DC (call this length a), CE = EA (call this length b) and AF = FB (call this length c). In other words, AB = 2c, BC = 2a and AC = 2b. The Triangle Mid-Segment Theorem states: In any triangle, a segment joining the midpoints of any two sides will be parallel to the third side and half its length. By this, FE = a, DF = b and FD = c.

Using Heron's formula, the area of triangle DEF is

.

The semiperimeter of triangle ABC is

.

Using Heron's formula to find the area of triangle ABC:

Thus, when P is the centroid of triangle ABC, the area of triangle ABC is 4 times the area of triangle DEF.