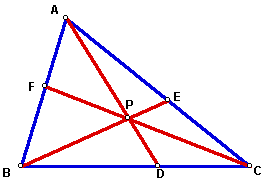

Conjecture:
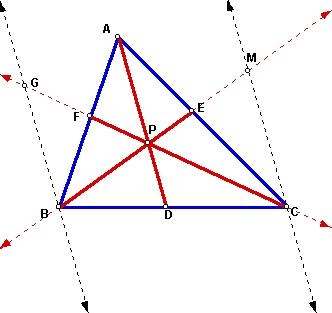
We begin by constructing two auxiliary lines parallel to segment AD through the vertices B and C. We then extend lines FC and BE to intersect these parallel lines at G and M respectively. The following similarities are apparent: triangle PDC ~ triangle GBC and triangle PDB ~ triangle MCB. Thus,
Solving the first equation for PD yields:
Substituting for PD in the second equation and simplifying:
The diagram also indicates that triangle BGF ~ triangle APF (Angles GFB and AFP are vertical angles and thus are congruent. Angles GBF and PAF are congruent because they are alternate interior angles formed by a transversal intersecting parallel lines. Therefore, triangle BFG ~ triangle APF by AA.) Triangles MCE and PAE are also similar. This implies that
Solving the equations for MC and BG respectively yields
We will take these expressions for BG and MC and substitute them into
Simplifying after the substitution results in
Mulitiplying both sides by (AE)/(CE):