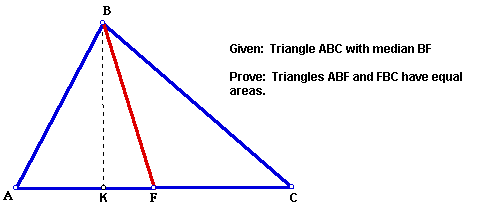
Theorem: Each median of a triangle separates that triangle into two triangles of equal area.

Proof:

(Auxiliary line segment BK has been constructed perpendicular to side AC) Since BF is a median of triangle ABC, F is the midpoint of AC and AF = FC. Both triangles BFC and ABF have the same altitude BK. Triangles ABF and BFC have the same base length and height and therefore the area of each triangle is the same.