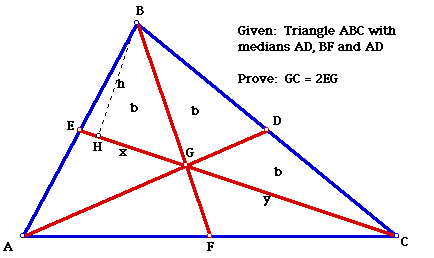
Theorem: The centroid of a triangle separates each median of that triangle into two smaller line segments whose lengths are in the ratio of 2:1.
Proof:

Explanation of variables: x = length GE; y = length GC; h = length BH; b = areas of triangles EBG, BGD and DGC (see theorem 2 on previous page for justification that these areas are equal.)
(Auxiliary line segment BH has been constructed perpendicular to line segment EC.) In the figure above, the area of triangle BGC equals twice the area of triangle BGE. Using the common formula for area of a triangle, 0.5hy = 2(0.5)hx. This equation simplifies to y = 2x, or GC = 2GE.
(Reference: Coxeter, H. S. M. & Greitzer,
S. L. (1967). Geometry Revisited. Washington D. C.: The Mathematical
Association of America.)
Return