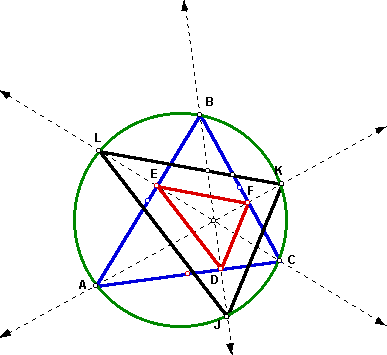
Problem: Examine the triangle formed by the points where the extended altitudes meet the circumcircle. How is it related to the orthic triangle?

In the diagram above, triangle ABC is the original triangle. Orthic triangle DEF, the circumcircle and triangle JKL formed by the points where the altitudes of triangle ABC extend to intersect the circumcircle have been constructed.

Conjecture: If triangle ABC is acute, then triangles JKL and DEF are similar and their sides are in the ratio of 2:1.

Click here for a GSP sketch to manipulate. Try dragging points A, B or C and notice the ratios of the sides of triangles JKL and DEF.