In this assignment we will be investigating some parametric equations. Let us start out with the following parametric equation and it's graph:


Both equations are being graphed with a=1, b=1, and t going from 0 to pi. Both equations with these parameters create a circle with center at the origin and a radius of 1. However, some neat things happen when we change the parameter a. For even values of a, we get parabolas created by portions of the cos wave with the number of parabolas being related to a by the following (a-1). For odd values of a, we get two symmetric cos waves about the y-axis, and the number of parabolas is equal to a. Let's look at a couple of graphs to illustrate this:

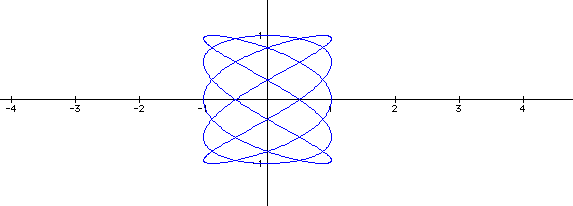
The first graph is for a=6 and the second graph is for a=5. Note, that both graphs have boundaries of 1 and -1 on both x and y axis. Now let's see what happens when we keep a=1 and vary b. It would seem we would get the same reaction only this time with the sin wave, let's see:


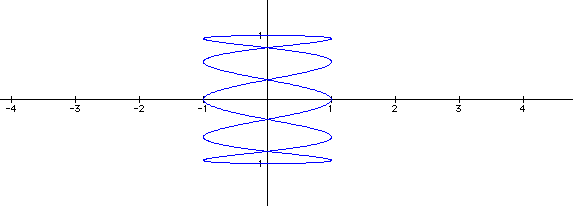
Well our hypothesis was proven wrong. The first graph is for b=6 and the second is for b=5. Two things have changed: 1. we always have symmetric waves, obviously it is the sin wave and the symmetry is now about the x-axis instead of the y-axis, 2. the number of parabolas created is always equal to b, whether b is even or odd. Note the occilations are still between 1 and -1 on both axes.
Let's explore one other parametric equation and it's graph:
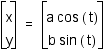
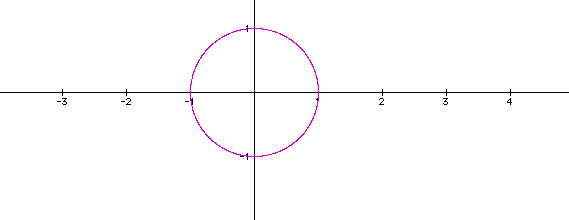
With our a and b parameters at 1 and t still ranging from 0 to pi, this new parametric equation also gives us a circle with center at the origin and radius of one. Now when we change the parameters of a and b, we get something quite different with this parametric equation then with the previous, let's look:


The first graph is for a=3 and the second graph is for b=2, it is clear that this new parametric equation creates ellipses instead of waves, and for the a parameter: the ellipse is bounded on the y-axis by 1 and -1 and bounded on the x axis by a and -a. For the b parameter: the ellipse is bounded by 1 and -1 on the x axis and by b and -b on the y axis. Some interesting relationships abound by the two different parametric equations and even within the individual equations themselves. Let's end by looking at a couple of graphs: the first will be of the first equation varying a and b, and the second will be of the second equation varying a and b: