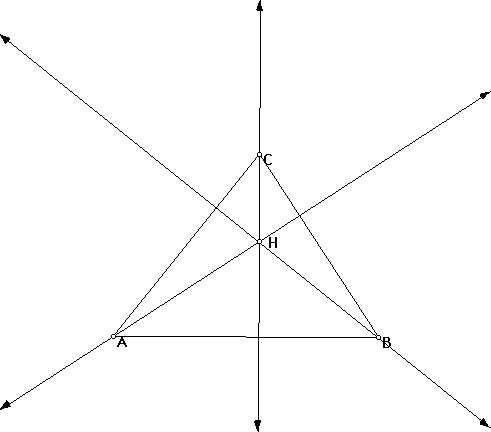
In this assignment, we are going to explore the altitudes of a triangle. First of all, the altitude of a triangle is a line that goes through a vertex of a triangle and is perpendicular to the opposite side. Let us now look at the construction of a triangle and it's altitudes:

It is clear from the above graph that the three altitudes are concurrent, that is they all intersect at the same point. This concurrent point of intersection, labeled H in the graph, is called the orthocenter. If you change the shape of the following triangle, you will see that there is always an orthocenter, indicating that for all acute triangles, the three altitudes will always be concurrent. Let us simplify the above diagram and look at some interesting properties of the orthocenter:

The first interesting property is that if we move the orthocenter to one of the vertices, we create a right triangle as the following graph shows:

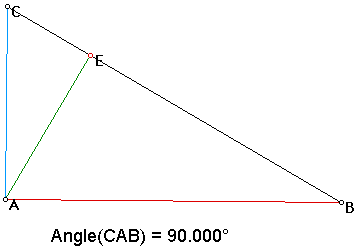
This graph shows that when the orthocenter becomes one of the vertices, H and G are concurrent with A, that the angle formed by the altitude and the leg of the triangle intersecting the altitude form a right angle, this has to be the case because when the orthocenter becomes a vertex, this forces the altitude to also become a leg of a triangle, making two legs of a triangle perpendicular, creating a right triangle. Another interesting property of the orthocenter is that it only stays inside of acute triangles, that is for obtuse triangles, the orthocenter lies outside of the triangle. This can be shown by taking the above right triangle and extending the orthocenter away form vertex A as so:

From the diagram it can be seen that as the orthocenter is taken outside of the triangle, our right angle from before becomes an obtuse triangle indicating that for obtuse triangles the orthocenter will lie outside of the triangle. One last interesting point about the orthocenter, is that when it leaves the an acute triangle, it always exits through one of the vertices, this is due to the properties of perpendicular lines. Your assignment is to use GSP, to explore the discussed properties of the orthocenter and through your exploration, intuitively show that these properties hold for various triangles.