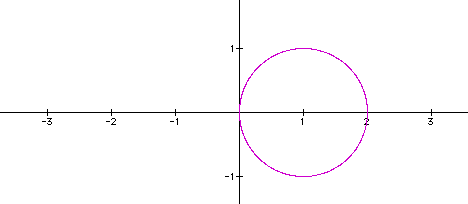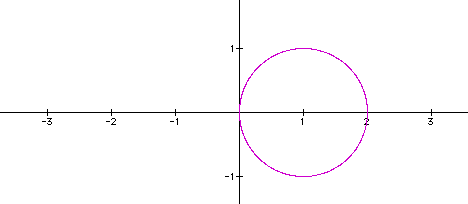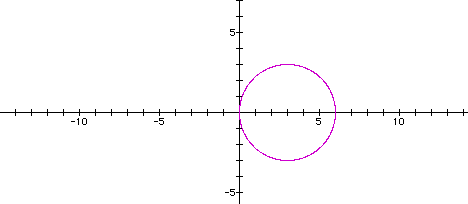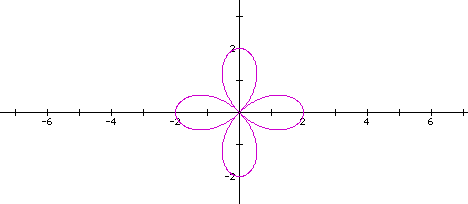Investigation of
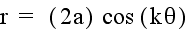
To start this investigation, again, we will look at the
graph of the above equation when a = 1 and k = 1.
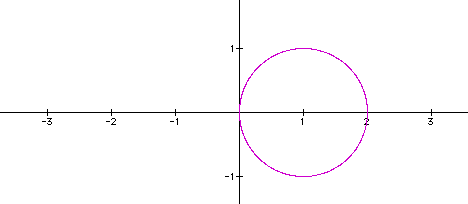Looking at this graph we see that equation is symmetric
around the x-axis and that it appears that the circle still has
a center of 1 on the polar scale.
To investigate further we will see what happens to
the graph when we vary the value of a...therefore let's explore
the graph of the equation when a = 3 and k = 1.
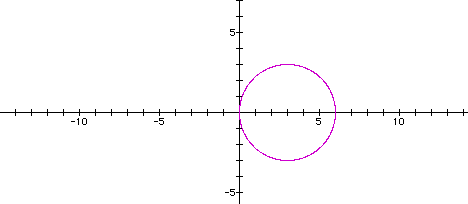It appears that the circle has expanded in this case
as well...it now appears that the center is equal to 3 on the
polar scale.
Now let's see what happens when we vary the value of
k...so let's look at what happens if a = 1 and k = 2
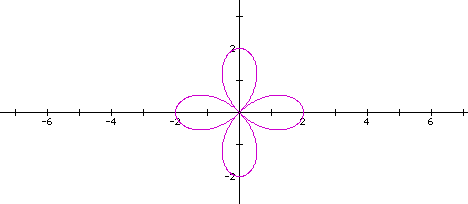It seems that once again if we allow k > 1 we get
a completely different type of graph...instead of a circle we
have pedals.
Since the graph has 4 pedals...we could possible
assume that k times 2 would equal the number of pedals.
Let's check to see if our theory for the sine
equation is the same as the cosine equation. Let's look
at another graph to check...how about when k = 5 and a is still
equal to 1.
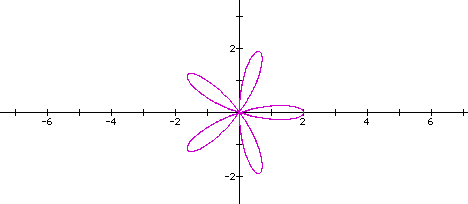Here it looks like the number of pedals equals the
value of k
Click on the links to see the graphs when k
= 4 and k = 7.
Yes, it appears that our theory for sine is the same
for cosine
After looking at these graphs we can assume that when
k is an even number, the number of pedals will be twice the value
of k. However, when k is an odd number, the number of pedals
is equal to the value of k.
So what is the difference in the equations...let's
look at the following graph for both the sine
equation and the cosine equation.
Now what happens when we vary both the values of "a"
and "k"?
Lets look when a = 3 and k = 5...if our assumptions
stand true we should get a graph with 5 pedals and the center
of the pedal being equal to 3.
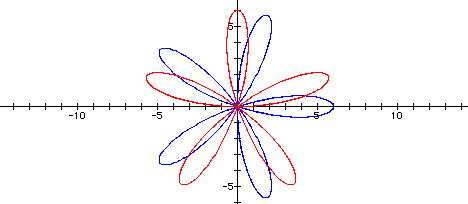Yep, not only do we have a graph with 5 pedals where
the center of the pedal appears to be 3 but looking at the graphs
overlapped we can also see that the cosine equations rotates the
graph to the right
Return to Assign 11