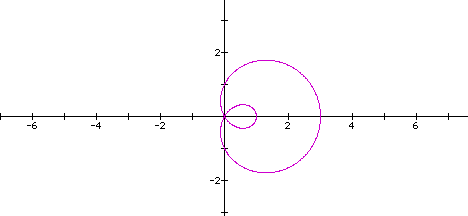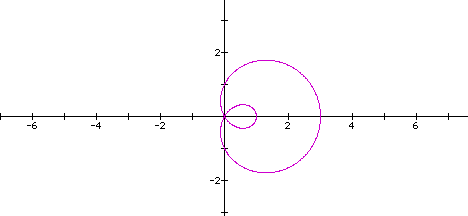Investigation of

To start this investigation, again, we will look at the
graph of the above equation when a = 1 and k = 1 and b = 1
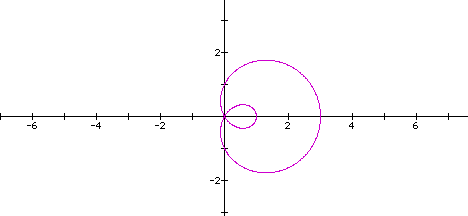 Again, we see that the equation is symmetric
around the x-axis, however it has a distinctly different shape.
There appears to be a smaller curve inside the larger one...how
will this change if we change the value of b.
To investigate further we will see what happens to
the graph when we vary the value of b...therefore let's explore
the graph of the equation when a = 1and k = 1 and b = 2.
Again, we see that the equation is symmetric
around the x-axis, however it has a distinctly different shape.
There appears to be a smaller curve inside the larger one...how
will this change if we change the value of b.
To investigate further we will see what happens to
the graph when we vary the value of b...therefore let's explore
the graph of the equation when a = 1and k = 1 and b = 2.
 It appears that the smaller curve has disappeared ...it
now appears that there is a bend in the larger curve.
Now let's see what happens when we vary both the value
of k and b...so let's look at what happens if a = 1, k = 2 and
b = 2.
It appears that the smaller curve has disappeared ...it
now appears that there is a bend in the larger curve.
Now let's see what happens when we vary both the value
of k and b...so let's look at what happens if a = 1, k = 2 and
b = 2.
 Not quite sure what is happening here...now we appear
to have 2 pedals connected at the origin...let's look if we vary
a as well; a = 2, k = 2 and b = 2.
Not quite sure what is happening here...now we appear
to have 2 pedals connected at the origin...let's look if we vary
a as well; a = 2, k = 2 and b = 2.
 Now we have 4 pedals with two of them smaller than
the original two...what happens when we make a = 5.
Now we have 4 pedals with two of them smaller than
the original two...what happens when we make a = 5.
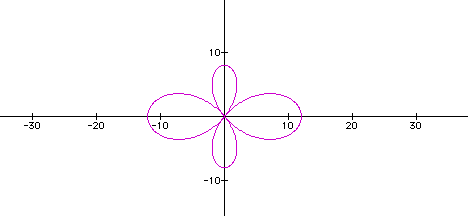 In this case it just appears that the shape of the
pedals expanded as it did in the previous investigation when we
changed the value of a...so let's change the value of k...let's
look at the equation when a = 2, k = 5, and b = 2.
In this case it just appears that the shape of the
pedals expanded as it did in the previous investigation when we
changed the value of a...so let's change the value of k...let's
look at the equation when a = 2, k = 5, and b = 2.
 Here it appears that we have 5 large pedals with 5
smaller pedals inside.
Here it appears that we have 5 large pedals with 5
smaller pedals inside.
Lastly let's vary all of the values...a = 3, b = 1, k = 5
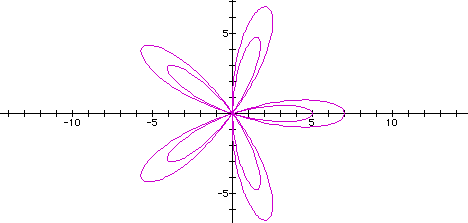 Playing around with different variables tends to lead
that one can make the assumption that the variable b determines
whether or not you have inside pedals
Playing around with different variables tends to lead
that one can make the assumption that the variable b determines
whether or not you have inside pedals
 In the above graph, a = 1, k = 5, and I have set b
equal to 1, 2,
3 and 4
All of this sounds exactly like
our sine equation investigation...again lets see how they differ
by overlaying the sine equation and cosine equation
This time we will let a = 3,
b = 2 and k = 4
In the above graph, a = 1, k = 5, and I have set b
equal to 1, 2,
3 and 4
All of this sounds exactly like
our sine equation investigation...again lets see how they differ
by overlaying the sine equation and cosine equation
This time we will let a = 3,
b = 2 and k = 4
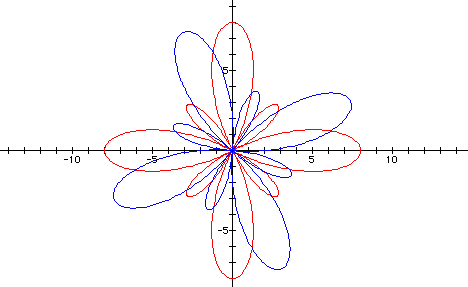 Again it looks like that the
cosine equation rotated the graph to the right.
Again it looks like that the
cosine equation rotated the graph to the right.
Return to Assign 11