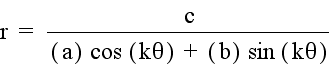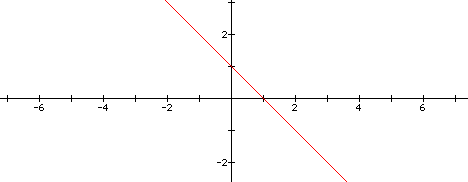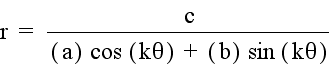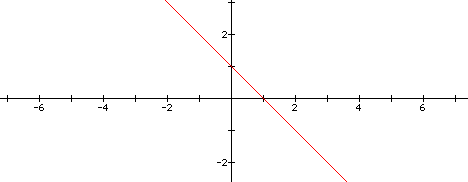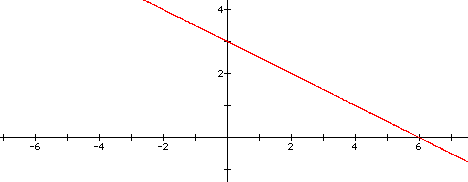Investigation of
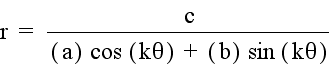
With this investigation we will look at the graph of the above
equation when a = 1, k = 1, b = 1 and c = 1
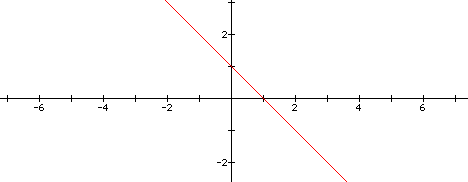 It appears to be a simple graph of a line...with the
x-intercept = 1, the y-intercept = 1, and the slope equalling
-1...what happens when we change the value of a to 4.
It appears to be a simple graph of a line...with the
x-intercept = 1, the y-intercept = 1, and the slope equalling
-1...what happens when we change the value of a to 4.
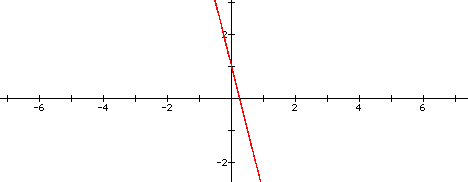 In this case it appears that the y-intercept is still
equall to 1 but the x-intercept is now 1/4...does this mean that
the y-intercept could be equal c/b or b/c and x-intercept equal
to either b/a or c/a? Let's explore this further by leaving
k = 1 but varying the other variables...how about a = 10, b =
20, and c = 60
In this case it appears that the y-intercept is still
equall to 1 but the x-intercept is now 1/4...does this mean that
the y-intercept could be equal c/b or b/c and x-intercept equal
to either b/a or c/a? Let's explore this further by leaving
k = 1 but varying the other variables...how about a = 10, b =
20, and c = 60
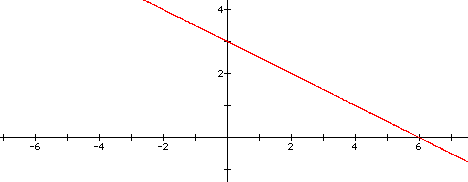 Here it appears that the x-intercept is equal to 6...which
would be c/a; and the y-intercept is equal to 3...which would
be c/b...Let's continue to explore this to see if our theory continues
to stand true. Let's look at when a = -5; b = 15, and c
= - 60
Here it appears that the x-intercept is equal to 6...which
would be c/a; and the y-intercept is equal to 3...which would
be c/b...Let's continue to explore this to see if our theory continues
to stand true. Let's look at when a = -5; b = 15, and c
= - 60
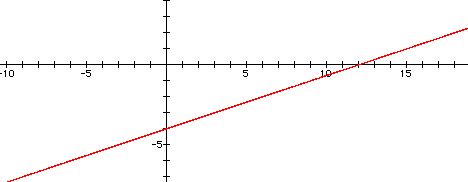 Yes, it looks to be true...the x-intercept is equal
to 12, the ratio c/a and the y-intercept is equal to -4, the ratio
c/b.
Now that we know how the graph changes with the variations
of the variables a, b, and c...let's see what happens when we
change the value of k.
Let's let a = 1, b = 1, c = 1, and k = 2
Yes, it looks to be true...the x-intercept is equal
to 12, the ratio c/a and the y-intercept is equal to -4, the ratio
c/b.
Now that we know how the graph changes with the variations
of the variables a, b, and c...let's see what happens when we
change the value of k.
Let's let a = 1, b = 1, c = 1, and k = 2
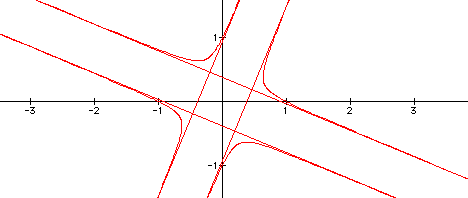 Oh my...look what we have...it appears that we have
four lines that form a rectangle (possible square) and then we
have what appears to be 4 parabolas...it also looks like the lines
that form the rectangle could also be asymptotes of the parabolas.
What happens when we change the value of k to 3?
Oh my...look what we have...it appears that we have
four lines that form a rectangle (possible square) and then we
have what appears to be 4 parabolas...it also looks like the lines
that form the rectangle could also be asymptotes of the parabolas.
What happens when we change the value of k to 3?
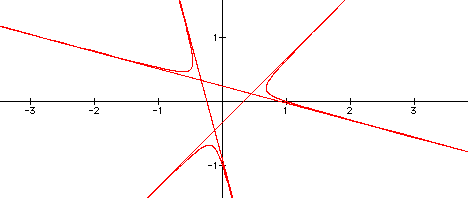 This time the lines form a triangle whose sides could
be asymptotes to the 3 parabolas that are formed.
Does this mean that the theory we saw in the very first
investigation continues to work here where if k is even the lines
of the graph will form a polygon with 2k number of sides and 2k
parabolas and if k is even the lines form a polygon with k number
of sides and k number of parabolas?
Let's look at a couple more graphs to see what happens.
a = 1, b = 1, c = 1, and k = 6
This time the lines form a triangle whose sides could
be asymptotes to the 3 parabolas that are formed.
Does this mean that the theory we saw in the very first
investigation continues to work here where if k is even the lines
of the graph will form a polygon with 2k number of sides and 2k
parabolas and if k is even the lines form a polygon with k number
of sides and k number of parabolas?
Let's look at a couple more graphs to see what happens.
a = 1, b = 1, c = 1, and k = 6
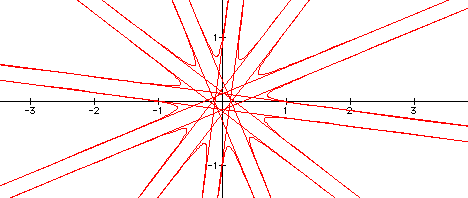 and
a = 1, b = 1, c = 1, and k = 9
and
a = 1, b = 1, c = 1, and k = 9
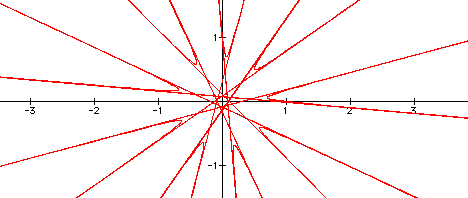 What do you think!!!!
What do you think!!!!
Return to Assign 11