Construction of Medial Triangle
by
Rita Meyers
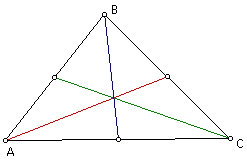
We start off with Triangle ABC and its medians.
Next I will construct a line.
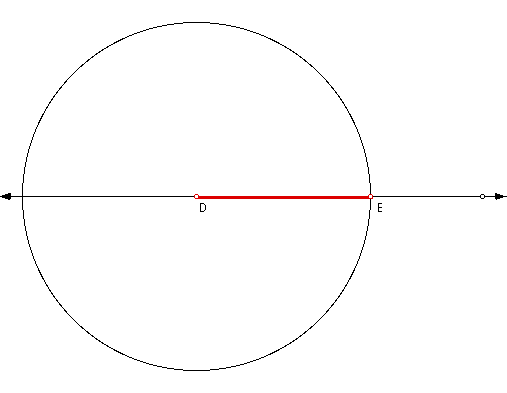
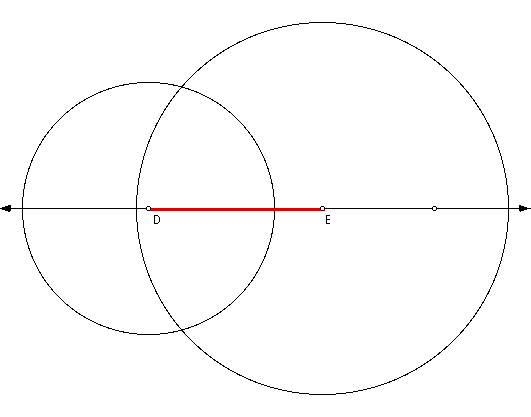
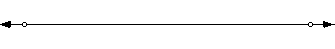Selecting any point on the line (identified
as D), construct a circle with the selected point on the line
being the center and the radius equaling the measurement of the
median from Vertex A.
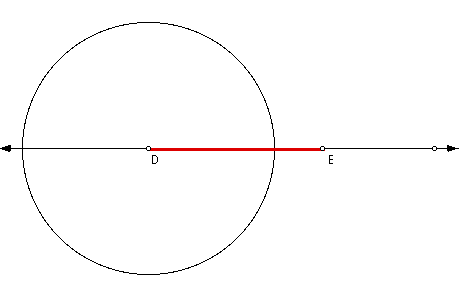
Also, construct a point on the line
where the circle intersects the line (identified as E).
The distance from the center (pt D) to the new point (pt E) is
the measurement of the median from Vertex A. This will be
the base of our new triangle.
Next, construct a circle with pt D
being the center and the radius equaling the measurement of median
from Vertex B.
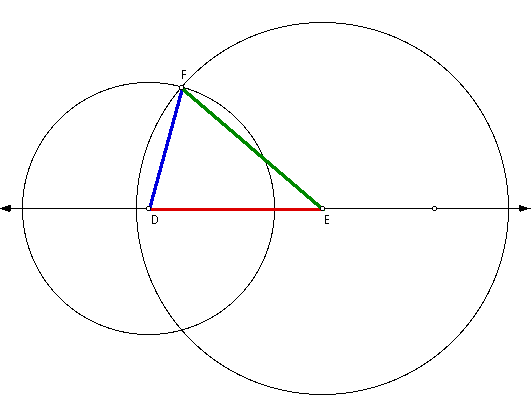
Then construct another circle with
pt E being the center of circle and the radius equaling the measurement
of median from Vertex C.
Construct a point on the line where
the two circles intersect (identified as F).
Then construct line segment DF and
line segment EF.
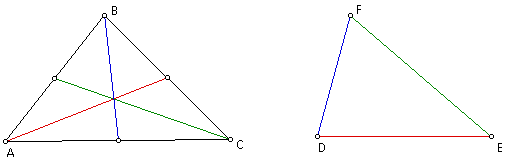
We have now constructed a triangle
whose sides are equal to the lengths of the medians of the original
triangle.
Return to Assign 6