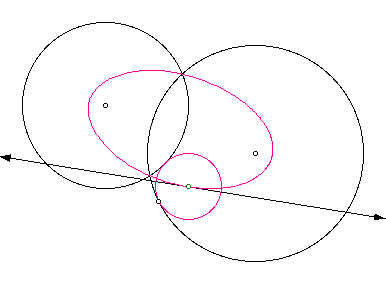Exploring Tangent Circles
by
Rita Meyers
During this exploration we will look at a circle
that is Tangent to two given circles.
We will look at this in several different ways.
The first case we will look at is if
one of the given circles is inside the second given circle.
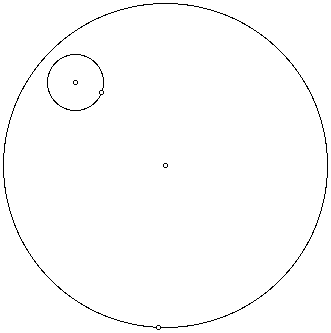
First we will explore what happens when the smaller given circle is external to the
tangent circle.
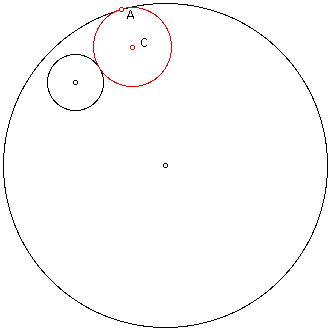In order to explore these circles let's
discuss the locus of the center of the tangent circle.
Exploration #1
If we move the tangent circle along the large
circle we see that the locus of the center of the tangent circle
looks like this
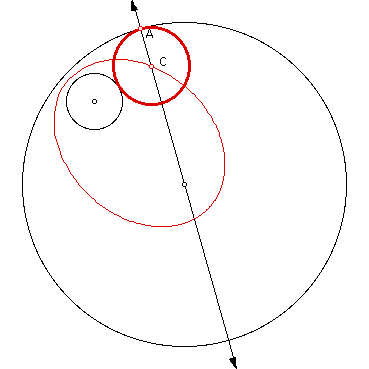and if we move the circle along the
small circle we get this locus
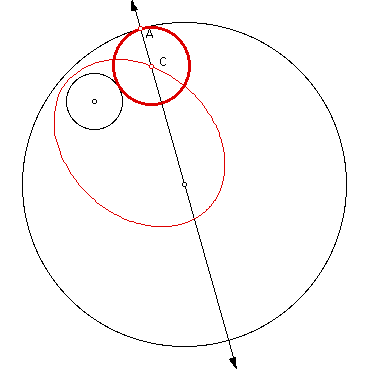In each case it appears that the locus
is an ellipse with the centers of the given circles your foci;
I'll go further to say that they are the same locus
What happens when the smaller
circle is internal to the tangent circle.
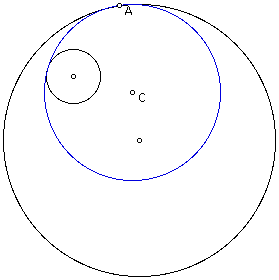Now, let's explore these circles by
discussing the locus of the center of the tangent circle.
Exploration #2
Again if we move the tangent circle
along the large circle we see that the locus of the center of
the tangent circle looks like this
And if we move the tangent circle along
the small circle we get the same locus; which again appears to
be an ellipse with the centers of the given circles your foci.
What happens if our two given circles
intercept (Use the same construction method as the given circle
internal to the tangent circle)?
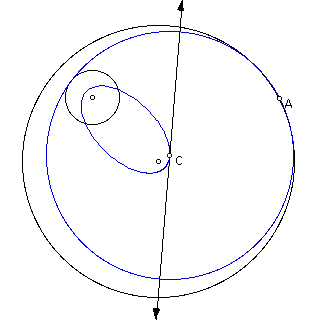
Let's again explore by discussing the
locus of the center of the tangent circle.
Exploration #3
Once more we have a locus that looks
like this.
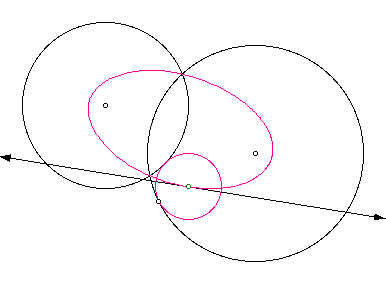If we move the tangent circle along
either given circle we get a locus that once again appears to
be an ellipse with the foci the centers of the given circles.
Lastly, we will look at what happens
if our given circles are completely separate of each other (Again,
use the same construction method as the given circle internal
to the tangent circle).
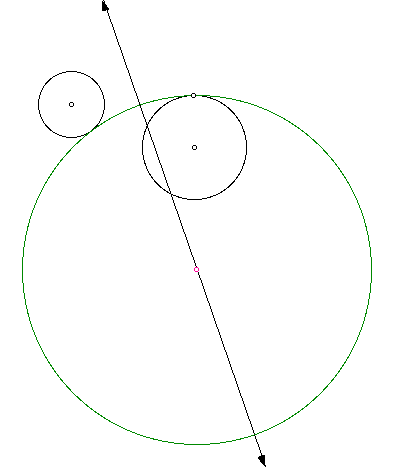We'll also explore this situation by
looking at the locus of the center of the tangent circle
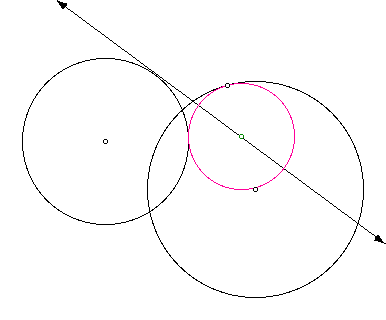
Exploration #4
Here we are a totally different locus
that previously; we now have one that looks like this.
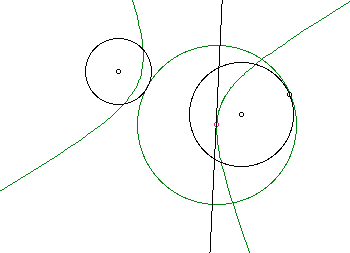When we move the tangent circle along
either given circle we get a locus that this time appears to be
a hyperbola with an asymptote
Return to
Rita's Page