Exploring Orthocenters
by
Rita Meyers
In this exploration we will look at an orthocenter
of a given triangle and some different investigations of the orthocenter.
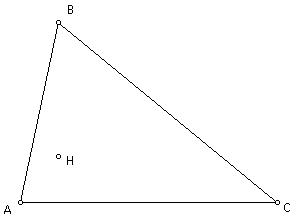
Let's start with a given triangle ABC
and it's orthocenter H.
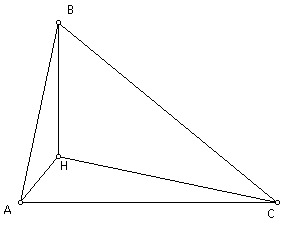
Now let's construct triangles HAB,
HBC, and HCA
We'll first explore these new triangles
by contructing the orthocenters of these three triangles
H' = Orthocenter of HAB
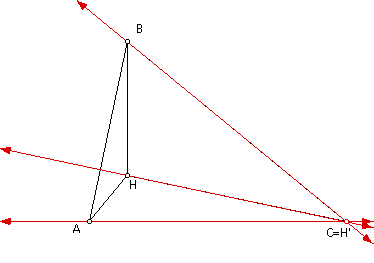
H'' = Orthocenter of HBC
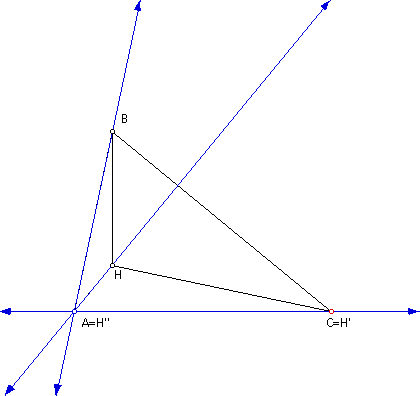
H''' = Orthocenter of HCA
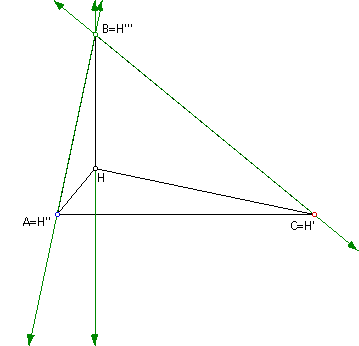Looking at the orthocenters of these
three triangles we see that each one correlates to a vertex of
the given triangle.
Next we'll explore further, by looking
at the circumcircles
First we will construct the circumcenter
of the given triangle in order to find the circumcircle.
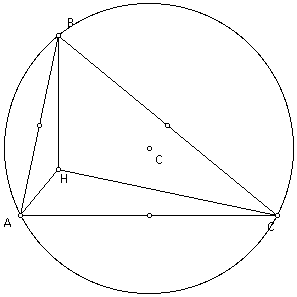Now let's construct the circumcircles
of triangles HAB, HBC, and HCA
Circumcircle of HAB
Circumcircle of HBC
Circumcircle of HCA
This is what we have
when we have the circumcircles of all four triangles.
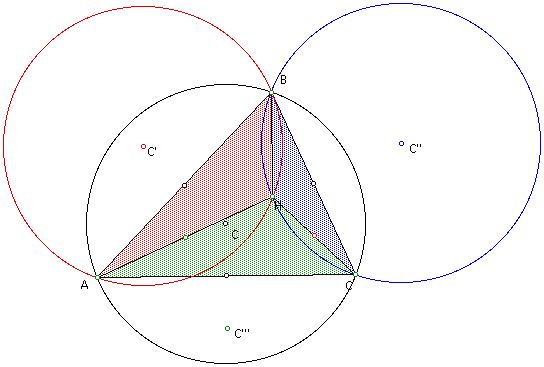Let's explore this
sketch
What happens when we make the
orthocenter (H) of the original triangle (ABC) equal to a vertex
of the triangle ABC (or an orthocenter of triangles HAB, HBC,
or HCA)?
If we move vertex B
so that it overlays the orthocenter H this is what we see
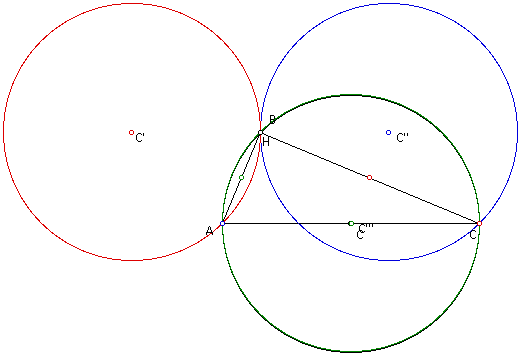It appears that the
circumcircle of triangle ABC is now equal to the circumcircle
of triangle HCA
Does this appear to
be the same when the orthocenter is equal the other vertices of
the original triangle
H = Vertex A
H = Vertex C
If fact it is true
that the circumcircle of the original triangle is equal to one
of the circumcircles of the triangles constructed with the orthocenter
H, when the orthocenter H is equal to one of the vertices of triangle
ABC
Return to Rita's Page