---

Exploring the Pedal Triangle
by
Rita Meyers

---

This exploration deals with the construction of a pedal triangle and investigating different aspects of it.

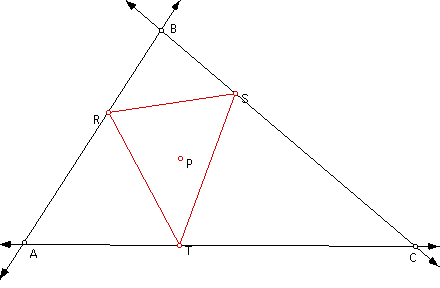
First given triangle ABC we must construct the Pedal Triangle RST

Now that we know how to construct a pedal triangle...what happens when you make the arbitrary point P equal to the incenter...the point inside of the triangle that is equidistant from all sides of triangle ABC.

Now we construct the incircle of triangle ABC...

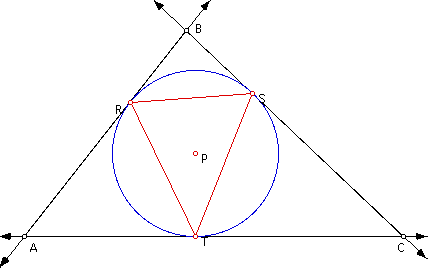If you look closely you will see that the incircle of triangle ABC is also the circumcircle of our pedal triangle RST
Exploration #1
We also notice that the pedal triangle and the pedal point never travel outside of the original triangle

What happens when the pedal point is also the circumcenter?

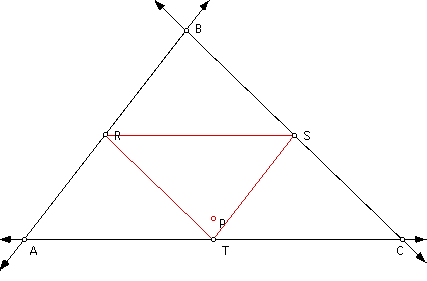Just by definition of a pedal triangle we can prove that the vertices of the pedal triangle are the midpoints of the sides of our original triangle ABC
Exploration #2
Again the pedal triangle never travels outside of the original triangle; however, the pedal point will exit triangle ABC through the vertices of the pedal triangle or the midpoints of triangle ABC

Now let's look if the pedal point is the centroid

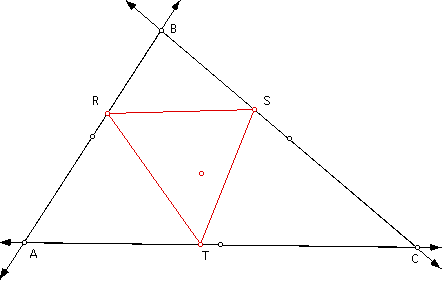Again while exploring we can see that the pedal triangle will never move outside of the original
triangle ABC
Exploration #3
Although the triangle never moves outside triangle ABC; you will notice that it can change from a triangle to simply a line segment

Lastly let's look at the pedal point being the orthocenter

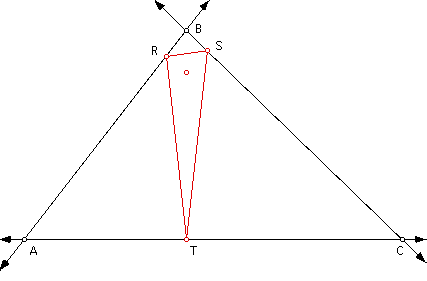If you look at the exploration we can see that the pedal triangle does move outside of the triangle ABC
Exploration #4
We can also see that the pedal point will always exit the original triangle through the vertices.  It also appears that when the pedal point becomes one of the vertices of the the original triangle that all three sides of the pedal triangle merge forming a segment

---

Return to Rita's Page

---