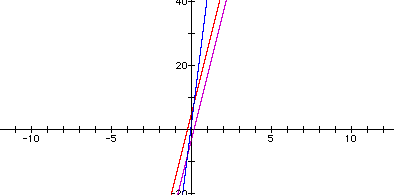We'll start by looking at the sum of the two equations
when n = 0; therefore:
f(x) = -3
g(x) = 5
h(x) = -3 + 5 therefore h(x)
= 2
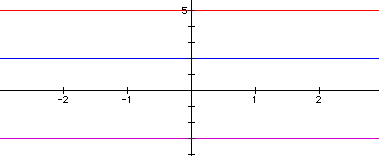
Here we notice that we get a line where the slope
is 0 and the y-intercept is 2, the sum of the y-intercepts of
f(x) and g(x)
What happens when we make n=6
f(x) = 6x - 3
g(x) = 6x + 5
h(x) = (6x - 3) + (6x + 5)
This time not only can we see
how the y-intercept of h(x) is equal to the sum of the y-intercepts
of f(x) and g(x), but also look closely at the slope. The slope
of both f(x) and g(x) is equal to 6 and the slope of h(x) is
the sum of the slopes of f(x) and g(x)
Does it always work that way...and
will h(x) always be a linear graph? Let's look once more with
n=20
f(x) = 20x - 3
g(x) = 20x + 5
h(x) = (20x - 3) + (20x + 5)
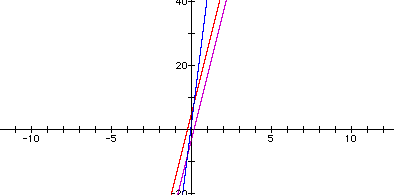
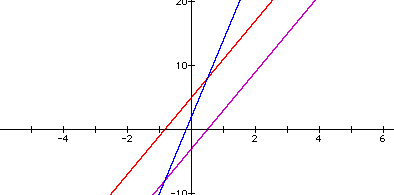
The y-intercept of h(x) = 2,
the sum of the y-intercept of f(x) and y-intercept of g(x) and
the slope is 40, the sum of the slope of f(x) and the slope of
g(x).
Now let's look closer at the
equation, will it always be linear
Consider:
f(x) = ax + b
g(x) = cx + d
Letting h(x) = f(x) + g(x);
h(x) = (ax + b) + (cx + d)
Using the communative property
we can obtain
h(x) = (ax + cx) + (b + d)
h(x) = (a+c)x + (b + d)
Since addition of real numbers
yield a real number we can say
m = (a + c)
n = (b + d)
Therefore, h(x) = mx + n
Therefore, h(x) is also a linear
equation whose slope is equal to the sum of the slopes of f(x)
and g(x), as is the y-intercept of h(x) equal to the sum of the
y-intercepts of f(x) and g(x)