Now let's investigate the product of f(x) and g(x)
when n = 0; therefore:
f(x) = -3
g(x) = 5
h(x) = -3 * 5 therefore h(x)
= -15
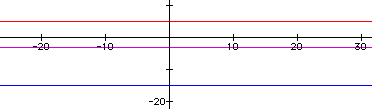
Again we get a straight line...will this continue?
What happens when we make n=6
f(x) = 6x - 3
g(x) = 6x + 5
h(x) = (6x - 3) (6x + 5)
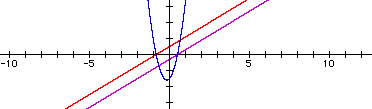
Here it looks like the product
of two linear functions equals a quadratic function...will this
be the trend?
Let's look once more with n=20
f(x) = 20x - 3
g(x) = 20x + 5
h(x) = (20x - 3) (20x + 5)
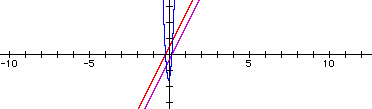
Yes, another quadratic function...let's
break it down to see if this will always happen.
Suppose:
f(x) = ax + b
g(x) = cx + d
where a,b,c and d are real
numbers
Letting h(x) = f(x) * g(x);
h(x) = (ax + b) (cx + d)
Using the FOIL
h(x) = (ax)(cx) + (ax)d + (cx)b
+ bd
where h(x) = y
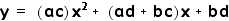
Since addition of real numbers
yield a real number we can say
p = ac
q = (ad + bc)
r = bd
such that p,q, and r are real
numbers
Therefore,
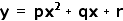
the general form of the quadratic
equation


