To continue with our investigation, let's look at
the quotients of f(x) and g(x) where
f(x) = -3
g(x) = 5
h(x) = -3/5
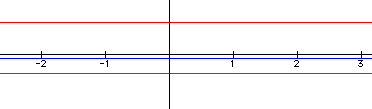
Again we start off with straight lines.
What happens when we make n=6
f(x) = 6x - 3
g(x) = 6x + 5
h(x) = (6x - 3)/(6x + 5)
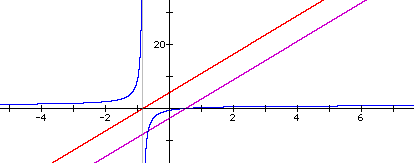
It appears that we have a hyperbola
instead of a straight line.
Let's check this out with n
= 20 to see if it is a trend
f(x) = 20x - 3
g(x) = 20x + 5
h(x) = (20x - 3)/(20x + 5)
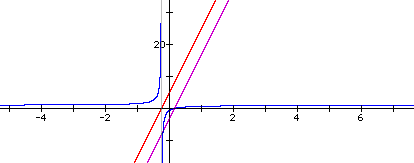
Not only do we get another
hyperbola, but it looks like in both cases where we had a hyperbola
that h(x) also has an asymptote
From what we know about functions,
we know that h(x) is discontinuous when its denominator is equal
to zero.
Therefore in the last case
h(x) is discontinuous when:
20x + 5 = 0
20x = -5
x = -5/20
x = -1/4
To see if there will always
be discontinuity let's look at the general case
f(x) = ax + b
g(x) = cx + d
h(x) = (ax + b)/(cx + d)
therefore the function would
be discontinuous when:
cx + d = 0
cx = -d
x = -d/c
Therefore, if f(x) and g(x)
are linear functions their quotient, h(x), will always have an
asymptote located at x = -d/c


