THE ANSWER TO THE MISSING BLOCK PUZZLE
The Answer in the book was:
There isn't an extra block. The area making the new
block was "shaved off" from some of the other blocks.
The loss of each block's area is so small that it's not easy
to observe.
That answer just didn't satisfy our curiositytherefore
we used GSP to explore the puzzle a little further.
First we wanted to explore what the book meant by
"shaved off"so we took the original 8 unit by 8 unit
square and color coded the pieces to get a better look at how
the pieces fit together.
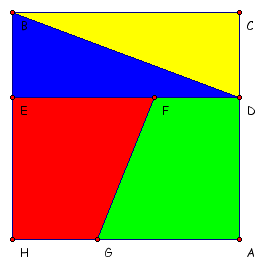
Using a grid with GSP we drew the 8 unit by 8 unit
square and then found the area of each piece and added them together
and indeed the area was 64 square units.
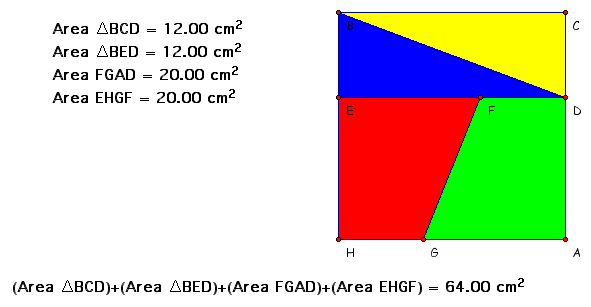
We then rearranged the square into the rectangle.
Obviously the area of each individual piece didn't change but
when we took the area of the rectangle it was 65 square units
instead of the 64 square units.
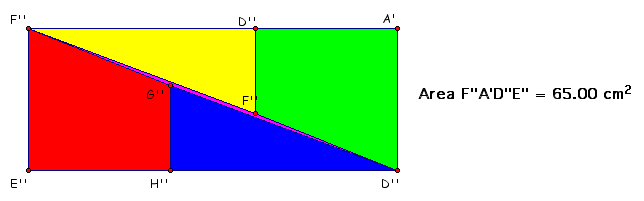
However; with the rearrangement on the grid it became
evident that the alignment of the pieces was off (which is not
as evident when just using paper and scissors). But why??
Finally we realized that when the pieces are cut that
the angle or slope of the two diagonal cuts must be the key therefore
we calculated the slopes of the angle cuts.
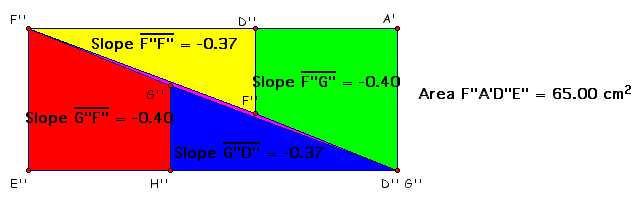
Sure enough the slopes of the trapezoids was a "shave"
larger than the slopes of the triangles. Which explains why the
pieces didn't match up perfectly. Although the pieces didn't
match up perfectly the little space didn't seem that it would
make exactly 1 square unit differentthis is where GSP came in
handyto try to accurately measure the area where the pieces didn't
come together by hand or by individual unit is nearly impossible.
However, with GSP we can form a new quadrilateral and find the
exact area.
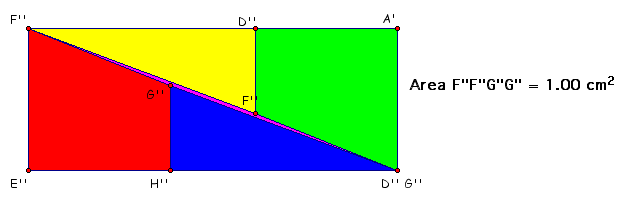
Now we can see and prove that the small area that
separates the original pieces does equal exactly 1 square unit
(although to the naked eye it doesn't seem that large)
And that is how an 8 unit by 8 unit square can be
rearranged into a rectangle and the area change from 64 square
units to 65 square units!!!





