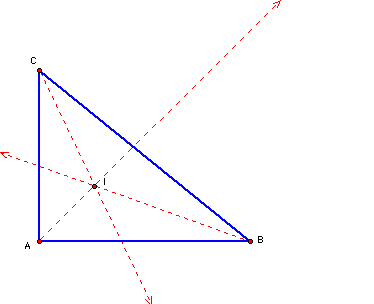
With the right triangle, the incenter stayed inside the triangle. It did move from its previous location in the acute triangle.

Once again, the incenter remained on the interior of the triangle. We will actually prove later that the incenter is equidistant from the three sides of the triangle. Therefore, the incenter must always be inside the triangle.