The Koch Snowflake is a fractal that is generated by the trisection of a line segment. I will attempt to illustrate step - by - step the process in which the Koch Snowflake is created. Step one, of course, is to trisect a line segment. This has already been discussed in an earlier essay, so I will forego the explanation of how this is done.

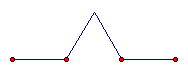
The middle 3rd segment is left out, while two segments congruent to the 1st and last segments are drawn to an intersection point above the missing segment. Next, we will iterate this figure to each 1/3 line segment from the figure above.

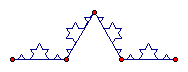
Next, the snowflake will be generated by using this iteration and forming a triangle with the endpoints.

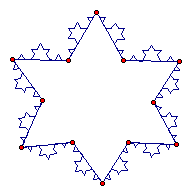
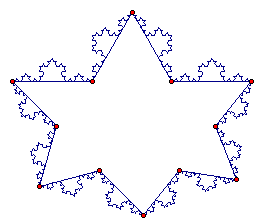
This is just one form of Koch's Snowflake. One could change the look to the snowflake by adding and subtracting the number of iterations done.

Look for and explore some fractals on your own. Try Sierpinski's Triangle, or others you may find.