The area of a parallelogram is very similar to that of a rectangle or square, especially since those two figures are both parallelograms. By definition, a parallelogram is a quadrilateral in which both pairs of opposite sides are both congruent and parallel. Obviously, the rectangle and square each have these properties. However, a parallelogram does not have to have right angles at each vertex. As the angles of a rectangle or square change and the sides remain constant, the area of the given parallelogram changes. In this section, we will explore the basic shape of a parallelogram, the area, the formula and then present some problems involving the area of parallelograms.

The base and height of a polygon meet at a right angle. Therefore, many times an auxillary line has to be added to a parallelogram in order to find the height. Let's let segment AB be the base of our parallelogram and construct an auxillary line that is perpendicular from AB to DC. This segment will be our height.

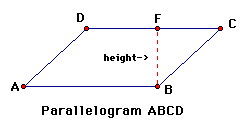
Segment BF is perpendicular to AB and DC, this segment may be used as our height. With a rectangle and square, each pair of consecutive sides meet at right angles, therefore, any two consecutive sides may be considered the base and height.

FORMULA: The formula for the area of a parallelogram is the exact same as that of the rectangle. The area is equal to the product of the base and the height of the parallelogram.(Make sure your base and height are perpendicular line segments.)

PROBLEMS: Solve the following problems. Show all work.

1) height = 10 cm, base = 4 cm, Area = ?

2) height = 2.9 m, base = 3.8 m, Area = ?

3) Find the Area of Parallelogram ABCD.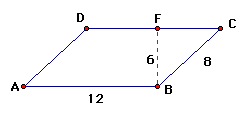

4) The area of a parallelogram is 84 sq.yds, the base is 4 yds, find the height.

5) The area of a parallelogram is 128 sq.ft., the height is 8 ft., find the base.