In this unit, we will look at finding the area
of shapes that are not seen on a regular bases and do not have
specific formulas in which to use. However, we will continue looking
at polygons.
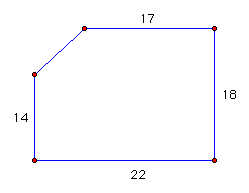
If we are given the following shape
and asked to find the area, we do not instantly think of a formula
to apply.
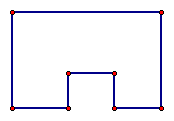
It is impossible to find a formula for every polygonal shape that can be created. Therefore, we will use formulas of the shapes we do have formulas for to find the area of any polygonal shape. Let's divide this shape into more familiar shapes by drawing auxillary lines and creating rectangles. We know how to find the area of rectangles.
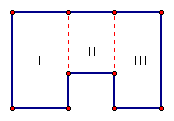
We will now use the area formula for a rectangle and find the areas for the three regions shown. By adding up the areas of the three regions, we will now have the total area of the polygon. We have constructed familiar, nonoverlapping polygons to find the area of a nonfamiliar polygon. This can be done with any polygonal shape.
Problems: Area of Nonoverlapping Polygons
1) Find the area.
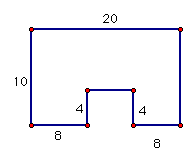
2)Find the area.
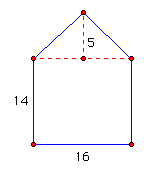
3) Find the area.