Problem 1 : A green on a golf course is in the shape of a circle. A golf ball is 8 feet from the edge of the green and 28 feet from a point of tangency on the green. Assume the green is flat.

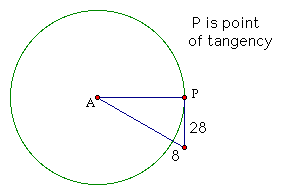
1) What is the radius of the green?

2) How far is the golf ball from the cup at the center A?

3) What is the area of the green?

Problem 2 : The town of Elizabethton, Tennessee, restored the roof of this covered bridge with cedar shanks, a kind of rough wooden shingle. The shakes vary in width, but the average width is about 10 inches. So, on average, each shake protects a 10 inch by 10 inch square of roof. An illustration of the roof is shown below with the back and left sides both hidden.

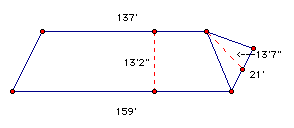
The dashed red lines represent height and the top and bottom of the roof are parallel.

1) The hidden back and left of the roof are the same as the front and right sides. Find the total area of the roof.

2) Estimate the number of shakes needed to cover the roof.